EMMOUNT Technologies, LLC
4329 Emerald Hill Circle
Canandaigua, NY 14450
Fairport, NY 14450
585/223-3996
585/919-6504, Fax
emmount@earthlink.net
September 17th, 2009
To Whom It May Concern
Customer A
Anywhere
Subject: Viscosity Measurements
Summary:
1. Five sample resins were received and measured with a capillary rheometer at 200, 225 and 250 C.
2. Next the raw data was reduced and Rabinowitsch corrected shear rates and viscosity values were calculated.
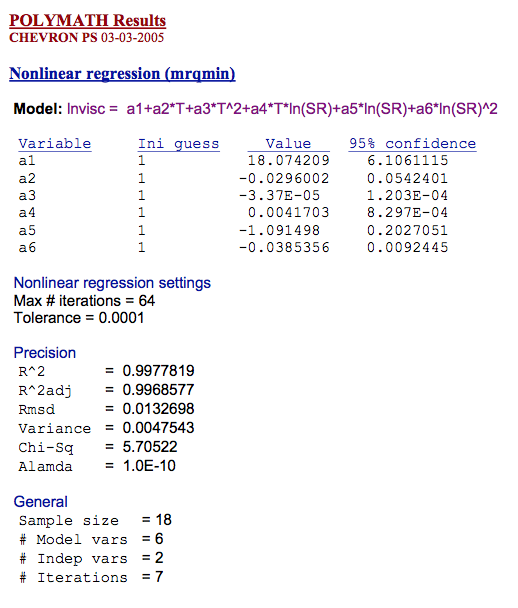
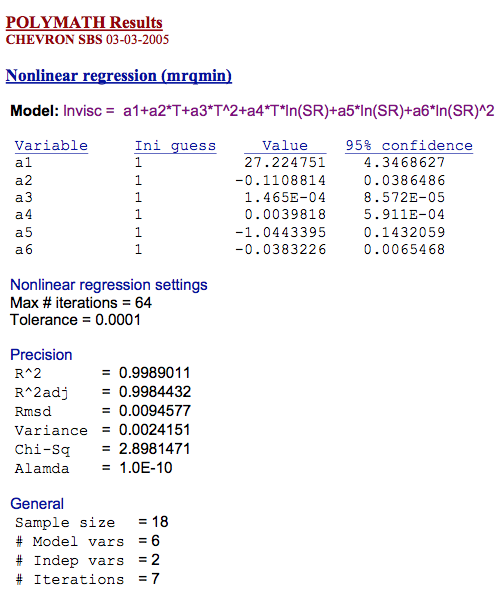
3. Corrected data was fit to a six constant curve fitting equation for the compact representation and easy manipulation of the results
a. Ln (η) = A1 + A2*T + A3*T^2 +A4*T*Ln(SR) +A5*Ln(SR) +A6*Ln(SR)^2
b. T= Temperature degrees C and SR = corrected shear rate sec-1
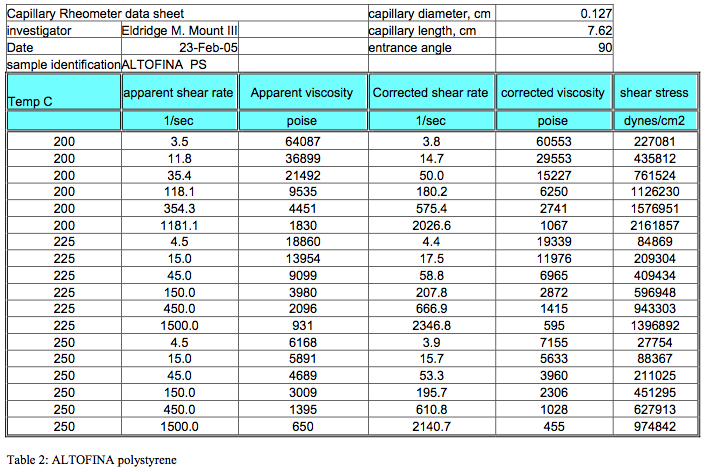
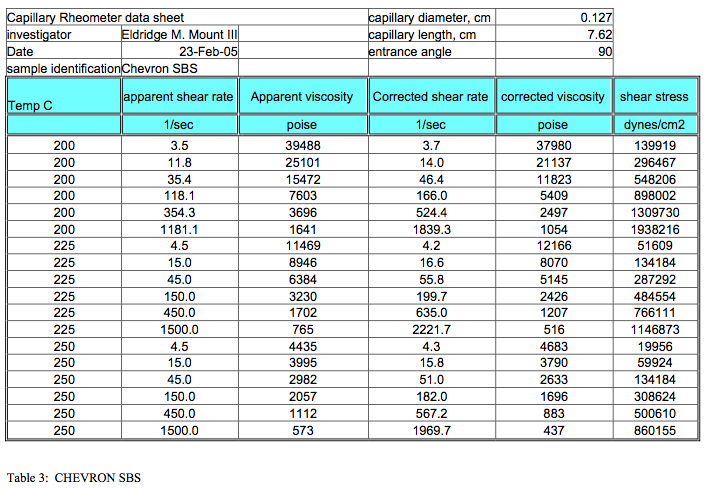
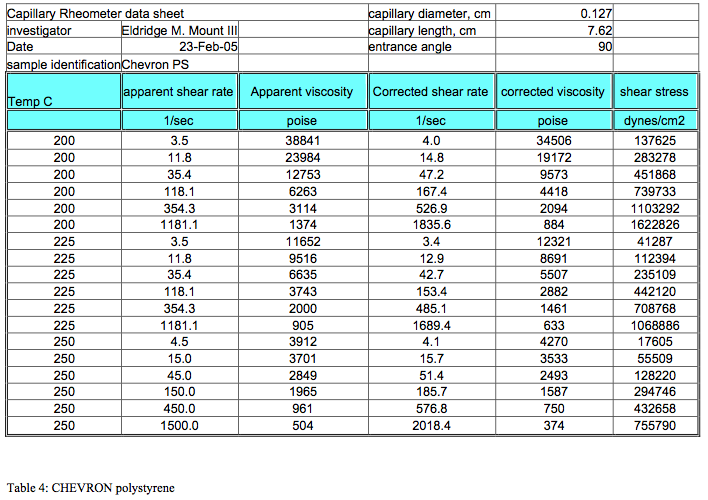
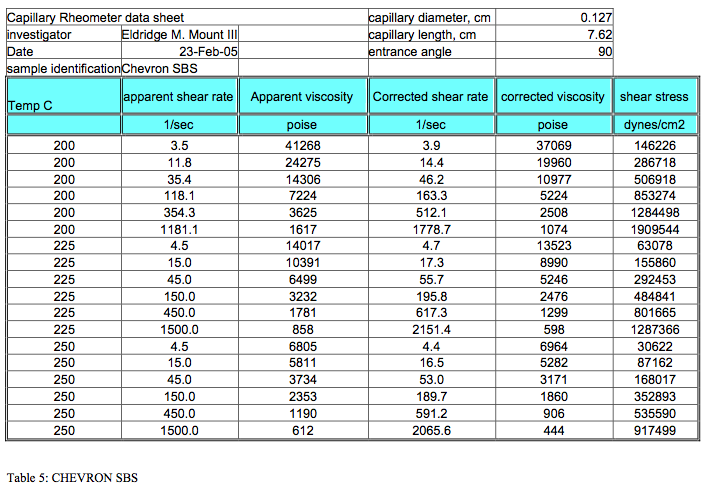
4. The calculated results are listed in Tables 2 through 6
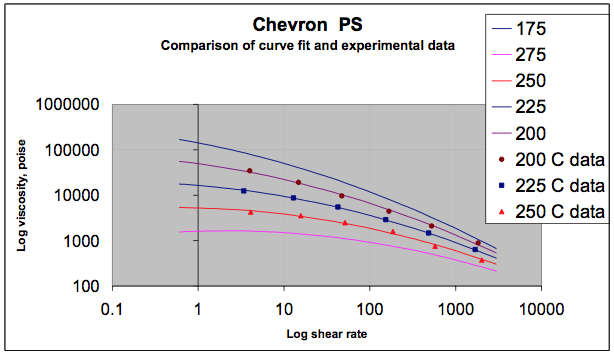
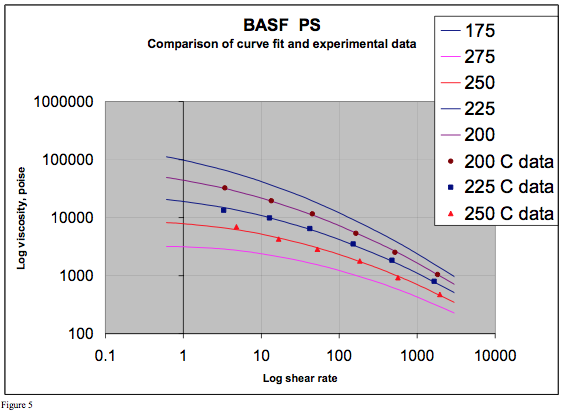
5. The experimental data and the curve fit results are compared in Figures 1 through 5 and represent the measurements very well.
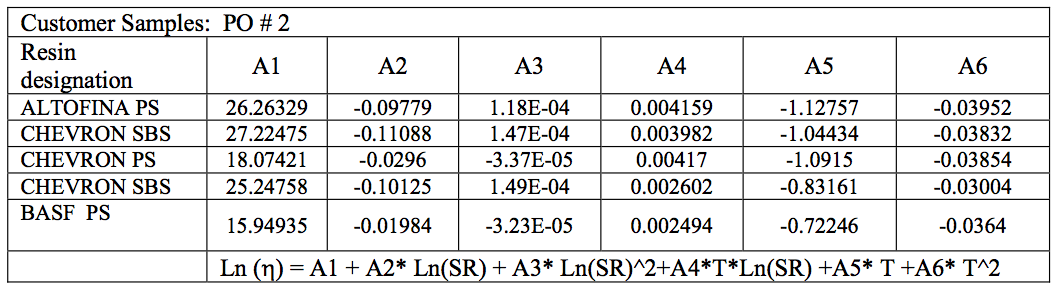
6. The Curve fitting Coefficients are:
Discussion:
Five samples of polystyrene and SBS polymer pellet were supplied for measurement. They were designated:
- ALTOFINA PS
- CHEVRON SBS
- CHEVRON PS
- CHEVRON SBS
- BASF PS
All samples ran well and showed no unusual flow behavior during the testing
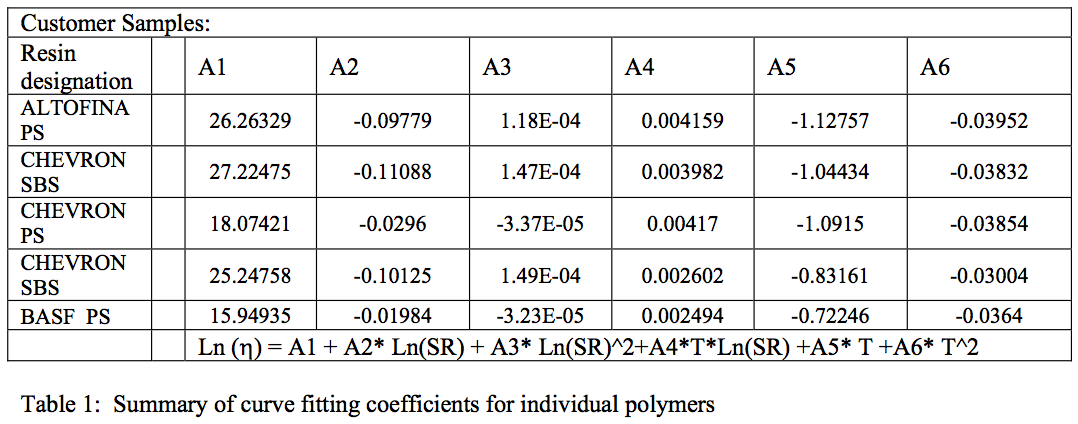
Table 1 lists the curve fitting constants for each of the individual resins tested
Curve fitting constants were calculated using POLYMATH, a commercially available nonlinear multiple regression software using the method of steepest decent of Marquart.
Tables 2 through 6 summarize the results of the viscosity calculations in tabular form for future review.
Figures 1 through 5 summarize the experimental data and plot the results from the curve fit equation to
permit an evaluation of the goodness of the fit for each curve fit. These figures show excellent agreement
between the curve fit and the experimental data. Curve fitting results obtained from POLYMATH are also
attached for review.
Measurement and calculations:
An Instron Capillary Rheometer Model 3211 was used to collect the data for these resins. This is a
constant speed rheometer where a ram forces polymer through a capillary at the bottom of a barrel full of
polymer. The force required to move the polymer at a constant volumetric flow rate is then a measure of
the viscosity of the fluid. This is in contrast to a melt indexer which measures volumetric flow rate at
constant stress (dead weight). A 0.0500-inch (.127 cm) by 3 inch (7.62 cm) long, 60 L/D capillary with a
90 degree entrance angle was used to minimize entrance pressure lose effects and consequently no Bagley
entrance pressure loss correction was necessary or applied. The Rheometer was set and run at 6 constant
cross head speeds to generate pressure readings at each temperature tested. For each resin tested two full
barrels full of material was extruded prior to any measurements to insure complete purging of the capillary
of material of a different resin or from a different temperature. This insured that the data collected
represented fresh polymer. Prior to beginning the experiments the rheometer was electrically calibrated
according to the instructions.
The apparent shear rate (SR
ap), stress at the wall (τ
w) and apparent viscosity (η
ap) were calculated from the
cross head speed, plunger force and capillary dimensions using the well-known relationships:
SR
ap= 4Q/πR
3τ
w = R ∆P/2L
η
ap = τ
w / SR
apThe Rabinowitsch correction was applied to the apparent date through the shear rate using equation:
SR = 1/πR
3*{3Q + ∆P dQ/d ∆P}
This can be rearranged to yield:
SR = Q/πR
3 {3 + dLn (Q)/dLn (∆P)} = (SR
ap/4) *{3 + dLn (Q)/dLn (∆P)}
The cross head and plunger force data are transformed into Q and ∆P data and plotted on a Ln Ln plot and
curve fit to a second order in ∆P, the resulting equation is differentiated and the vales for dLn (Q)/dLn (∆P)
calculated at each point and the corrected shear rate is determined.
Ln (Q) = B0 + B1* Ln(∆P) + B2* Ln(∆P)
2dLn (Q)/dLn(∆P) = B1 + 2*B2* Ln(∆P)
Once the corrected shear rate is know the corrected viscosity is calculated from:
η = τ
w / SR
The results of the calculations for each resin at all three temperatures measured are tabulated and attached.
The viscosity is presented in Poise and the stress data are tabulated in dynes/cm
2.







Return to
Technical Articles.