Navigation¶

Extrusion 1-0-Wiki Pages

• Main Page
• Best Papers
• Book Reviews
• Consultants Corner
• Extruder Software
• Extrusion Hints
• Safety
• Shop Tools
• Sponsors
• Technical Articles
  

Search the Wiki
»

Viewing/Creating

• Random Page
• Create a new Page
• All Pages
• Categories
  

Account Management

• Login/Logout
• Language Selection
• Your Profile
• Create Account
  

Administration

• Administration
• File Management
  

Brought to you by:
The SPE Extrusion Division
Board of Directors

Evaluation of 9-Layer Film Blowing Process by Using Variational Principles

Evaluation of 9-Layer Film Blowing Process by Using Variational Principles¶

Martin Zatloukal^1,2, Roman Kolarik^1
1 Centre of Polymer Systems, University Institute, Tomas Bata University in Zlin, Nad Ovcirnou 3685, 760 01 Zlin, Czech Republic
² Polymer Centre, Faculty of Technology, Tomas Bata University in Zlin, TGM 275, 762 72 Zlin, Czech Republic

Abstract¶

In this work, coextrusion experiments utilizing an industrial 9-layer Brampton Engineering coextrusion film blowing line for LDPE/LDPE/tie/PA6/EVOH/PA6/ /tie/LDPE/LDPE film production has been performed under different processing conditions (different air cooling intensity and mass flow rate) in order to evaluate variational principles based modeling approach for the multi-layer film blowing process. It has been revealed that the variational principle based model can describe the bubble shape, temperature profile and predict internal bubble pressure reasonably well for all applied processing conditions even if the multi-layer film has been viewed as the static elastic membrane characterized only by one material parameter - bubble compliance J, which was not allowed to vary along the multi-layer bubble.

Introduction¶

Production of thin polymer films is mostly introduced by the film blowing process. Although this process is widely used, the single layer films do not reach specific properties required especially in a food packaging industry, such as barrier properties (low permeability to oxygen or carbon dioxide), heat-seal ability, high film strength, printability, adhesion and low costs [1-2]. All these properties are easily and economically achievable in multi-layer films produced by coextrusion.

In coextrusion, two or more different polymer melts (having various rheological properties and temperatures) are extruded from individual extruders, through a coextrusion die, to a continuous tube which is cooled by an air ring and internal bubble cooling system, IBC, axially stretched by the take-up force, F, and circumferentially inflated by the internal bubble pressure, Δp, to required bubble dimensions. Then, above the freezeline height, the stable solidified bubble is folded by the collapsing frames and consequently drawn upward by the nip rolls to a wind-up roll. Then, the final lay-flat coextruded multi-layer film, which represents a combination of the best properties of each used polymers, can be applied for example in food packaging, medical and electronic industry. The most frequently used materials in coextrusion are polar barrier polymers, such as nylon (PA), ethylene vinyl alcohol (EVOH), polyvinylidene chloride (PVDC), and nonpolar polyolefines, i.e. polyethylene (PE), polypropylene (PP), polystyrene (PS) [1-2].

In spite of a rapid growth of a blown film coextrusion in the last decades, the number of experimental and modeling studies of the multi-layer process is very limited. In 1978, Han and Shetty [3] experimentally and theoretically investigated blown film coextrusion of two polymers in various combinations, i.e. low density polyethylene (LDPE) with ethylene-vinyl acetate (EVA), LDPE with high density polyethylene (HDPE), LDPE with polypropylene (PP) and HDPE with EVA. Further, they performed a theoretical study where the experiment was theoretically analyzed by using a power-law nonNewtonian model included in a computational procedure predicting the number of layers, layer thickness and the volumetric flow rate compared with the experiment. Theoretical investigation of two-layer coextruded blown film was also studied by Yoon and Park [4] in 1992. In their work, considering isothermal processing conditions, two film layers are described by a Newtonian and an Upper-Convected Maxwell fluid (UCM). In order to evaluate influence of viscous and viscoelastic forces on the flow mechanics of the process, the various flow rate ratio values of the fluids are applied for numerical determination of the bubble radius and the film thickness profiles. It was revealed, that in the case of the small relaxation time the flow mechanics of UCM layer is similar to a Newtonian single-layer. On the other hand, increasing relaxation time supports the viscoelasticity effect of the UCM layer leading to dominance of bubble dynamics. In 2000, Yoon and Park [5] performed a linear stability analysis of the above presented polymer system. It was observed that the critical film thickness decreases with increasing blow-up ratio which makes the process unstable. In more detail, in case of a Newtonian single-layer flow, there exists an upper unstable region where the bubble is unstable when the BUR is greater than a certain critical value. On the other hand by the presence of a thin viscoelastic layer this restriction can be removed resulting in enhanced stable area at higher values of BUR. In 2000, Stasiek [6] studied the heat transfer between three-layer blown film and cooling medium. In his work, mathematical model, estimating length of a cooling path and taking into account crystallization effect, was developed and used to describe the relationship between the temperature changes in each layer and the thermal energy. In 2005, Elkoun et al. [7] investigated effect of composition and layout of layers on end-use properties of a coextruded LLDPE five-layer blown film. For coextruded structure, a conventional Ziegler-Natta LLDPE gas phase butene copolymer, an advanced Ziegler-Natta LLDPE solution octene copolymer, and a single site LLDPE solution octene copolymer were used and compared with monolayer blended film. It was observed, that combination of the LLDPE butene and the single site LLDPE in a fivelayer coextruded film reveals improved tear resistance due to a presence of interfacial transcrystalline layers. Further, combination of coextruded single site LLDPE and the Ziegler-Natta octane copolymers leads to enhanced tear strength, too. Finally, significant haze reduction, caused by placing the single site LLDPE on the outside layers of the multi-layer films, was observed. In 2005, Gamache et al. [8] performed experimental and theoretical study evaluating stresses in a two-layer coextruded blown film of LDPE, ultra low density polyethylene (ULDPE), LDPE/ULDPE and ULDPE/LDPE. Then, the axial and transverse stresses were experimentally measured under various processing conditions, which were then successfully compared with theoretically calculated ones by the non-isothermal Newtonian model. In 2007, Gururajan and Ogale [9] studied effect of coextrusion on the orientation and morphology of the coextruded films of PP and LDPE by using Raman spectroscopy. In the case of multi-layer films, no significant difference in overall molecular orientation of PP and LDPE was found. On the other hand, single-layer LDPE films indicated existence of some row-nucleation of crystals which was not observed in the LDPE layer in coextruded film. In 2009, a 2-D model describing non-isothermal two-layer blown film process was developed by Xu and McHugh [10]. This model is based on the 1-D model of Henrichsen and McHugh [11] taking to account viscoelasticity and flowenhanced crystallinity. The 2-D model presents numerical results showing influence of the rheological, thermal and crystallization properties on the crystallinity development and stresses in particular layers. It was observed, that the individual layers of the same materials contain significantly different stresses due to the temperature difference. Further, different material properties in a certain layer affect stresses and crystallinity in its own layer as well as in another layer through heat transfer. Finally, stresses and semicrystalline phase orientation at the freezeline, i.e. final film properties, are affected by the layer arrangement.

As can be seen from the literature overview, the number of theoretical studies of the multi-layer film blowing process is rather rare, considering maximally 3 layers and laboratorial processing conditions only due to extremely high mathematical and rheological complexity of the problem. Due to this, the multi-layer film blowing process for high number of layers and industrial processing conditions is not fully understood yet. Recently, it has been found that utilization of the variational principle based single-layer film blowing process modeling leads to very stable numerical schemes allowing qualitative as well as quantitative description of the experimental reality [12-18]. The main goal of this work is to investigate whether it is possible to utilize the variational principles based modeling approach for the multi-layer film blowing process. For the model validation purposes, industrial 9 layer film blowing line has been utilized to produce multi-layer bubbles under different processing conditions.

Mathematical Modeling¶

Zatloukal-Vlcek Formulation
The variational principle based Zatloukal-Vlcek formulation [12] describes a stable film blowing process as a state when the bubble shape satisfies minimum energy requirements (here the bubble energy is given by the elastic strain energy increase due to take up force and negative work done by the applied internal load). The bubble shape is described by a set of simple analytical equations (see Table 1) utilizing four physical parameters: the freezeline height, L, the bubble curvature, pJ (which is given by the membrane compliance, J, and the internal load, p, representing the internal force acting on the bubble length due to Δp – see Eq. 6), the inner die radius, R₀ and the blow-up ratio, BUR. It should be mentioned that the equations describing the freezeline height (Eq. (7)) and the temperature profile (Eq. (8)) have been derived in [13] from the cross-sectionally averaged energy equation [19] neglecting axial conduction, dissipation, radiation effects and crystallization. The particular symbols with respect to model equations summarized in Table 1 have the following meaning: C_p represents the specific heat capacity, HTC is the heat transfer coefficient, m is the mass flow rate, T_melt(die) represent the die exit melt temperature, T_solid is the solidification temperature and T_air is the cooling air temperature. Parameter φ is defined according to Table 2 where a parameter A is defined by Eq. (4).

Experimental¶

In this work, coextrusion experiments were carried out on an industrial 9-layer Brampton Engineering coextrusion film blowing line (Figure 1) equipped with a 350 mm diameter flat spiral die (R0 = 0.1626 m) with a die gap of 2.032 mm (H0 = 0.002032 m). During the process, the bubble was cooled by an air ring as well as by an internal bubble cooling system. The coextruded structure was LDPE/LDPE/tie/PA6/EVOH/PA6/tie/ /LDPE/LDPE with following layer thicknesses: 17.5 % for LDPE, 5% for tie, 5% for PA6 and 10% for EVOH. In all experiments, the following parameters were kept to be constant: die exit temperature, Tdie = 250°C, overall film thickness (gauge), H1=100 μm, (which corresponds to draw-down ratio DDR = 11.17), blow-up ratio, BUR = 1.8, and lay-flat film, 1000 mm. During the experimental work, firstly, different bubble cooling intensity was applied at the constant overall mass flow rate, 300 kg/h, (i.e. constant line speed 25.9 m/min) and secondly, overall mass flow rate was varied from 225 kg/h to 375 kg/h (i.e. from 19.4 m/min to 32.3 m/min for the line speed) by keeping the bubble cooling intensity the same. For given processing conditions, the bubble shape was monitored by the EOS digital SLR photo camera Canon EOS 450D model (Canon, Inc., Japan) with resolution of 12.2 Mpx equipped with Canon lens EF-S 18-55mm f/3.5-5.6 IS whereas the average bubble temperature was measured by the heat gun, model camera: INFRACAM^TM using calibration site FLIR SYSTEM, AB SWEDEN and corresponding software (ThermaCAM QuickReport 1.0).

Results and Discussion¶

At the beginning, three unknown film blowing model parameters L, BUR and pJ (for the known die radius R0 = 0.1626 m) were determined through fitting of all experimentally obtained bubble shapes by Eq. (8) utilizing the least square minimization method and they are summarized in Table 3. In order to calculate the takeup force and the internal bubble pressure for given processing conditions, p and J parameters were separated from the particular pJ value in the same way as described in [12] i.e. parameter J (which is viewed as constant characterizing the bubble compliance) was determined from pJ value for one reference processing conditions for which the load p was chosen to get equal predicted and measured internal bubble pressure. The reference processing conditions are provided in the second column of Table 3.

The comparison between the experimentally determined bubble shape and internal bubble pressure for all tested processing conditions are summarized in Figures 2-3 and Table 3, respectively, and as it can be seen, the agreement between the measured data and model fits/predictions is very good. In more detail, the model can describe the bubble shape as well as temperature profile along the bubble and predict internal bubble pressure reasonably well for both, decreased freeze line height and the bubble curvature due to increased air cooling intensity or decreased mass flow rate under highly non-isothermal conditions, even if the assumption about the constant bubble compliance J along the multi-layer bubble has been used. The fact that the single parameter J works could be explained by the statement that the layers which freezes first in coextrusion dictates the bubble shape [20-21]. This suggests, that the variational principle based modeling approach proposed in [12] can be used and explored for the multi-layer film blowing process in the similar way as shown in [12] for single-layer film blowing process. Moreover, it is believed, that such theoretical approach can be used to understand complex heat transfer and crystallization effects occurring in multi-layer film blowing process resulting in highly non-linear average temperature profile along the multi-layer bubble, depicted in Figures 2c and 3c for the studied experimental conditions, which is not the case of the single-layer film blowing process at which the average temperature profile along the bubble is almost linear as shown in [22-29].

Conclusion¶

In this work, coextrusion experiments utilizing an industrial 9-layer Brampton Engineering coextrusion film blowing line for LDPE/LDPE/tie/PA6/EVOH/PA6/tie/ /LDPE/LDPE film production has been performed under different processing conditions (different air cooling intensity and mass flow rate) in order to evaluate variational principles based modeling approach for the multi-layer film blowing process.

It has been revealed that the variational principle based model can describe the bubble shape, temperature profile and predict internal bubble pressure reasonably well for both, decreased freeze line height and the bubble curvature due to increased air cooling intensity or decreased mass flow rate under highly non-isothermal conditions even if the multi-layer film has been viewed as the static elastic membrane characterized only by one material parameter - bubble compliance J, which was not allow to vary along the bubble. Thus, it is believed, that the variational principle based modeling approach can be used and explored for the multi-layer film blowing process to understand complex rheological, heat transfer and crystallization phenomena occurring in multi-layer film blowing process with respect to process stability and final film properties.

Acknowledgments¶

The authors wish to acknowledge the Grant Agency of the Czech Republic (grant No. P108/10/1325) for the financial support. This article was written with support of Operational Program Research and Development for Innovations co-funded by the European Regional Development Fund (ERDF) and national budget of Czech Republic, within the framework of project Centre of Polymer Systems (reg. number: CZ.1.05/2.1.00/03.0111).

The authors would also like to thank Brampton Engineering Inc. which allowed us to perform all experimental work on their complete commercial size 9- layer AeroFrost air cooled blown film line.

References¶

1. Cantor, K. Blown Film Extrusion. Munich: Carl Hanser Verlag, 2006. ISBN 3-446-22741-5.
2. Butler, T.I. Film Extrusion Manual: Process, Materials, Properties. Atlanta: Tappi Press, 2005. ISBN 1-59510-075-X.
3. Han, C.D., Shetty, R., Polym. Eng. Sci. 1978, vol. 18, no. 3, pp. 187-199.
4. Yoon, K.S., Park, C.W., Polym. Eng. Sci. 1992, vol. 32, no. 23, pp. 1771-1777.
5. Yoon, K.S., Park, C.W., J. Non-Newtonian Fluid Mech. 2000, vol. 89, no.1-2, pp. 97-116.
6. Stasiek, J., Prog. Rubber Plast. Recycl. Technol. 2000, vol. 16, no. 3, pp. 183-192.
7. Elkoun, S., Huneault, M.A., McCormick, K., Puterbaugh, F., Kale, L., Polym. Eng. Sci. 2005, vol. 45, no. 9, pp. 1222-1230.
8. Gamache, E., Agassant, J.F., Demay, Y., Lafleur, P.G., J. Plast. Film Sheeting 2005, vol. 21, no. 2, pp. 127-144.
9. Gururajan, G., Ogale, A.A., J. Plast. Film Sheeting 2007, vol. 23, no. 1, pp. 37-49.
10. Xu, F., McHugh, A.J., Chem. Eng. Sci. 2009, vol. 64, no. 22, pp. 4787-4795.
11. Henrichsen, L.K., McHugh, A.J., Int. Polym. Proc. 2007, vol. 22, no. 2, pp. 179–189.
12. Zatloukal, M., Vlcek, J., J. Non-Newton. Fluid Mech. 2004, vol. 123, no. 2-3, pp. 201-213.
13. Kolarik, R., Zatloukal, M., J. Appl. Polym. Sci. 2011, vol. 122, no. 4, pp. 2807-2820.
14. Kolarik, R., Zatloukal, M., AIP Conference Proceedings 2009, vol. 1152, pp. 251-269.
15. Zatloukal, M., Kolarik, R., Annual Technical Conference - ANTEC, Conference Proceedings 2009, vol. 3, pp. 1587-1595.
16. Zatloukal, M., Kolarik, R., Annual Technical Conference - ANTEC, Conference Proceedings 2011, vol. 2, pp. 1317-1322.
17. Kolarik, R., Zatloukal, M., AIP Conference Proceedings 2011, vol. 1375, pp. 56-74.
18. Kolarik, R., Zatloukal, M., Martyn, M., International Journal of Heat and Mass Transfer 2013, vol. 56, no. 1, pp. 694-708.
19. Doufas, A.K., McHugh, A.J, J. Rheol. 2001, vol. 45, no. 5, pp. 1085-1104.
20. Morris, B.A., Journal of Plastic Film and Sheeting, 1999, 15(1), 25-36.
21. Giriprasath, G., Ogale, A.A., Annual Technical Conference – ANTEC, Conference Proceedings, 2006, 2, 830-834.
22. Wagner, M.H., Ph.D. Thesis, IKT Stuttgart, 1976.
23. Fisher, E., Ph.D. Thesis, IKT Stuttgart, 1983.
24. Cao, B., Sweeney, P., Campbell, G.A., J. Plast. Film Sheeting 1990, vol. 6, no. 2, pp. 117-130.
25. Kanai, T., White, J.L., Polym. Eng. Sci. 1984, vol. 24, no. 15, pp. 1185-1201.
26. Ast, W., Ph.D. Thesis, IKT Stuttgart, 1976.
27. Muslet, I.A., Kamal, M.R., J. Rheol. 2004, vol. 48, no. 3, pp. 525-550.
28. Beaulne, M., Mitsoulis, E., J. Appl. Polym. Sci. 2007, vol. 105, no. 4, pp. 2098-2112.
29. Sarafrazi, S. Sharif, F., Int. Polym. Proc. 2008, vol. 23, no. 1, pp. 30-37.


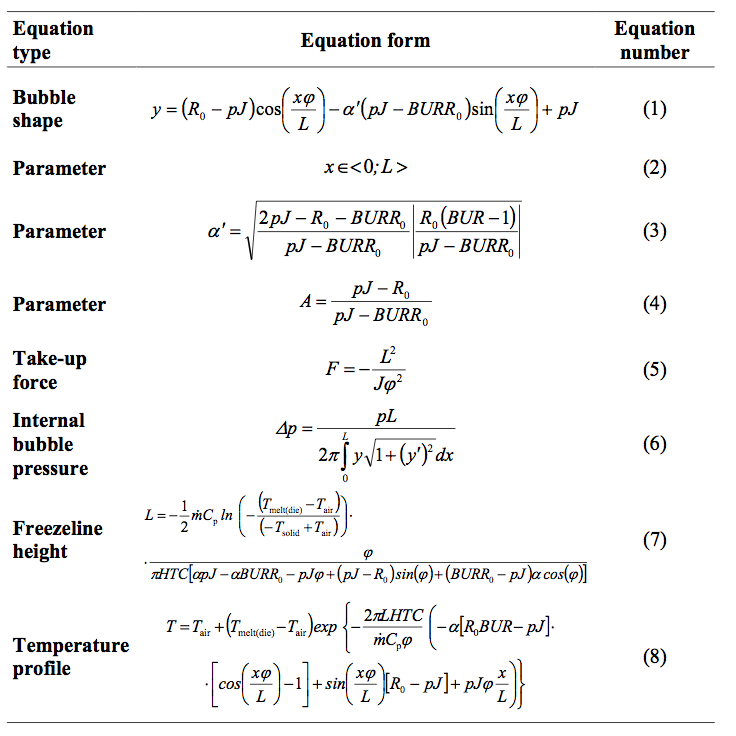
Table 1. Summary of the Zatloukal-Vlcek film blowing model equations [12-13].


Table 2. Parameters A and φ for different bubble shapes (y) [12].


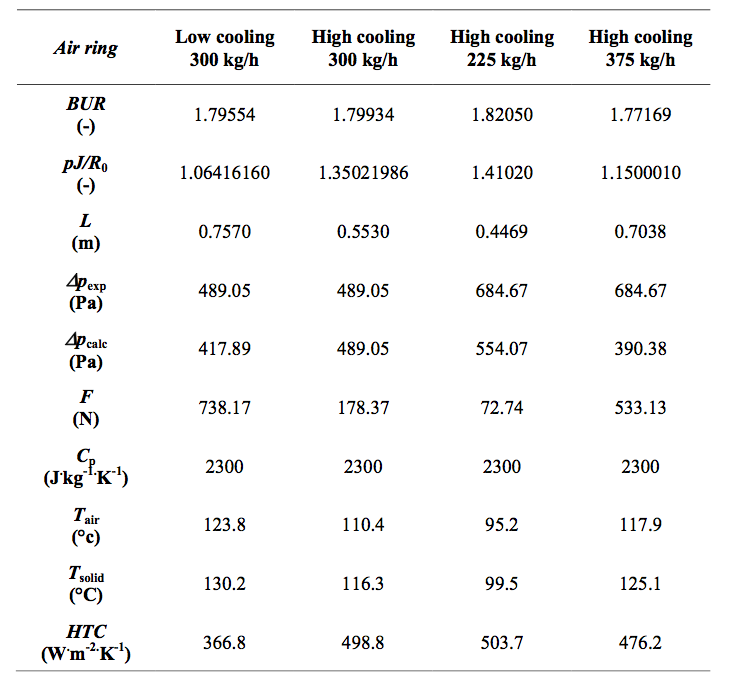
Table 3. Summarization of the model parameters and model predictions (by keeping the bubble compliance J the same for all the cases equal to 0.00028221 Pa-1) for all tested processing conditions including the measured value of the internal bubble pressure Δpe_xp.


Figure 1. Brampton Engineering 9-layer air cooled blown film line. 1a) Side view. 1b) Detail view of the 9-layer film formation at multi-layer die exit region including the scale for precise bubble shape determination by using digital image analysis.


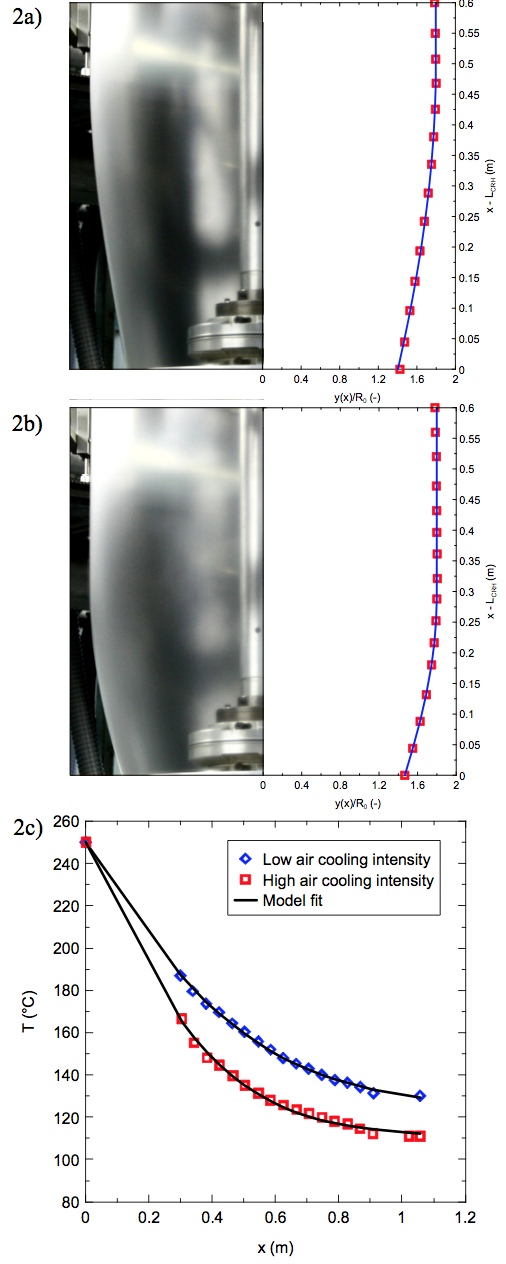
Figure 2. Comparison between experimentally determined multi-layer bubble shape and temperature profile (open symbols) and model fits (lines) for different air cooling intensity and fixed mass flow rate equal to 300 kg/h (cooling ring height, LCRH = 0.26 m). 2a) Bubble shape for low air cooling intensity. 2b) Bubble shape for high air cooling intensity. 2c) Temperature profiles for both applied air cooling intensities.


Figure 3. Comparison between experimentally determined multi-layer bubble shape and temperature profile (open symbols) and model fits (lines) for different mass flow rates and fixed air cooling intensity (cooling ring height, LCRH = 0.26 m). 3a) Bubble shape for mass flow rate equal to 225 kg/h. 3b) Bubble shape for mass flow rate equal to 375 kg/h. 3c) Temperature profiles for both applied mass flow rates.

Return to Paper of the Month.