Strand cooling
Vol. 9 #2, July 1980
Question:
Using the extrusion of fifty 1/8" diameter LDPE strands at a rate of 1500 lbs./hr. into a water bath, please provide a method for sizing the bath and a method of calculating the necessary heat transfer into the water. Would the effects of creating turbulent water contribute significantly to the cooling effect and where would you suggest the water enter the bath?
- Raymond Malinowski, Niles, MI 49120
Answer:
This is an unsteady-state heat transfer problem and could be solved in a straightforward manner except that the thermal properties of plastics, and particularly the properties of crystalline or partially crystalline materials cause some difficulties. For a material having a thermal conductivity independent of temperature and where no crystallization or glass transition is encountered, solution of unsteady-state heat transfer is encountered, solution of unsteady-state heat transfer in a cylindrical strand involves the solution of the differential equation derived by Craslaw and Jaeger (1).
Solutions to this equation are available in graphical form in (1) and Chapman (2). However, we find that µ is greatly affected by temperature since the thermal conductivity, density and specific heat of polyethylene are strongly dependent on temperature and
This can be handled approximately by taking a mean value of µ over the temperature range of interest or more precisely by using a numerical integration technique such as that of Crank and Nicoloson (3) with µ expressed in an algorithm as provided by Dietz (4) for a .914 g/cc density polyethylene.
A further complication arises because of the latent heat of fusion released when polyethylene is cooled below its crystal line melting point. Modification of the differential equation is required to take his into account and is handled by introducing another term involving the rate of neat release due to crystallization as indicated below.
(Eq. 3)
Again, we must use a numerical integration technique with the change of

and Cp being expressed by appropriate algorithms. Q, the rate of heat release due to crystallization is more difficult to handle because we find that the rate of crystallization of a polymer is affected by the rate of quenching, the molecular weight and molecular weight distribution, formulating additives, chain branching and orientation induced by drawing from the die orifice. One method, which is too lengthy to describe here, has been developed by Sifleet, Dinos and Collier (5). This technique takes into account all the factors mentioned with the exception of draw orientation.
Solution of Eq. 3 also requires establishing the rate of heat flow at the polymer/water interface. This can be described by:
(Eq. 4)
where h, the surface heat transfer coefficient is determined by first calculating the length Reynolds number:
(Eq. 5)
This type of flow becomes fully turbulent at a length Reynolds number of 500,000. Next, the heat transfer coefficient at the surface is calculated by:
(Eq. 6)
The term
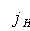
must be obtained from a plot of
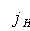
vs. length Reynolds number which can be found in Bird, Stewart and Lightfoot (6).
For the conditions outlined, it is found that the flow becomes fully turbulent 3 1/2 feet after entering the water bath. Creating additional turbulence would provide very little improvement in cooling rate. Also it is best to avoid providing a turbulent stream where the strands enter the bath since excessive turbulence here will cause the strands to touch and fuse together. Many operators prefer to use warm water in this region to avoid excessively fast quench rates which can result in shrinkage voids in the pellets.
Since counter-current flow is most efficient in heat transfer processes, cooling water should enter the bath where the strands exit. However, since we generally do not experience a large temperature rise in the water, we would not expect a great change in cooling efficiency regardless of where the water enters the bath. A more important consideration is to provide at least 1" of foam insulation on the cooling tank surfaces. It is not uncommon to find that under conditions where condensate forms on the tank surfaces, 50% of the heat load is caused by heat transfer to the atmosphere.
For crystalline materials, the procedure for calculating the heat transfer from the strands may be summarized as follows:
1. Using Equations 5 and 6 the chart in Ref. 6, determine the heat transfer co efficient at the surface, h.
2. Using Equations 3 and 4 and the method of Sofleet (ref. 5) calculate strand temperature as a function of time in the cooling bath. This involves using the Crank and Nicolson (Ref. 3) numerical integration procedure which requires a computer program and can not be illustrated here.
3. Choose a satisfactory strand exit temperature and determine the time required to reach that temperature. The length of bath required is then the product of the strand velocity and the cooling time required.
For amorphous materials we find the solution is simplified by the fact that no heat of crystallization is released. We still have to contend with the changes in density, thermal conductivity and specific heat with polymer temperature and the fact that these properties go through an abrupt change at the glass transition temperature.
However, we can get a fair approximation by using the mean values over the temperature range of interest.
For example, suppose we wish to extrude rigid PVC at 1500 lbs./hr using fifty Vs inch diameter strands, with a melt temperature of 380° F and a water bath temperature of 60° F. We wish to determine the length of bath required to cool the Center of the strand to 120° F.
The procedure is outlined in Chapman (Ref. 2) and requires the use of graphs in Chapman and Bird (Ref. 6). The mean properties of water over the temperature range of interest are:
The properties of PVC are:
REFERENCES:
(1) Carslaw, H. S. and Jaeger, J. C., Conduction of Heat in Solids, Oxford University Press, London.
(2) Chapman, A. J., Heat Transfer, 3rd Ed. Macmillan Pub. Co., N.Y., pp 137-146.
(3) Crank, J. and Nicolson, P., Proc. Cambridge Philos. Soc., Vol. 43, pp. 50-67 (1947).
(4) Dietz, W., Pol. Eng. and Sc, Vol. 18, pp. 1030-1036, (Oct. 1978).
(5) Sifleet, W. 1., Dinos, N. and Collier, J. R., Pol. Eng. and Sci., Vol. 13, No. 1 January 1973, pp. 10-16.
(6) Bird, Stewart and Lightfoot, Transport Phenomena, pp. 407-411.
The strand velocity is 13.62 in/sec.
Procedure:
1. Compute the length Reynolds number:
In this type of flow, complete turbulence
occurs when ReL = 500,000 or
L 500,000/7898
L = 63 inches from bath entry.
2. Compute the surface heat transfer coefficient, h. Note that since the Reynolds number varies along the length of the strand, h will also vary and we will have to again use a mean value of h along the length. The heat transfer coefficient is calculated using values of

from Bird (Ref. 6) page 410 and by equation 6. The mean value for h is found to be
3. Compute the Biot Number
4. Compute the relative temperature when the center of the strand reaches 120 F.
5. Using Fig. 4.15 from Chapman (ref. 6) we interpolate the line for

and find the corresponding Fourier Number (NFo) to be 0.62 when
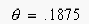
Since
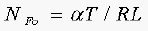
Cooling time,
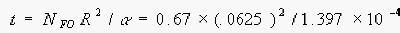
t = 17.3 sec
6. The length of cooling tank required is:
Lt = Vt = 13.62 x 17.3 = 234 inches
or 19.5 ft.
It is recommended that the calculated length be increased by 25% to account for the portion of the strand cooled under laminar flow conditions and also to take into consideration errors introduced by using mean property values.
- Leonard F. Sansone
|
Symbol |
Definition |
Units |
|
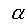
|
Thermal diffusivity |
in2/sec |
|
A |
Surface area |
in2 |
|
Cp |
Specific heat of polymer |
BTU/lb°F |
|
f |
Subscript indicating fluid property |
|
|
h |
Heat transfer coefficient |
BTU/sec in2°F |
|
jH |
Dimensionless correlation coefficient |
|
|
k |
Thermal conductivity |
BTU/sec in2°F |
|
L |
Distance along strand measured from entry into water bath |
in |
|
NF |
Viscosity of cooling fluid |
lbf sec/in2 |
|
ReL |
Length Reynolds number |
|
|
Q |
Rate of heat release due to crystallization |
BTU/sec |
|
Qs |
Rate of heat transfer at surface of strand |
BTU/sec |
|
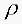
|
Density |
lb/in3 |
|
r |
Radial position in strand |
in |
|
T |
Temperature |
°F |
|
Ts |
Surface temperature of strand |
°F |
|
T |
Bulk temperature of cooling fluid |
°F |
|
t |
Time |
sec |
|
V |
Velocity of strand through cooling fluid |
in/sec |
|
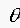
|
Relative temperature |
|
|
NBi |
Biot number |
|
|
NFO |
Fourier number |
|
|
R |
Radius of strand |
in |
See also:
- On/off barrel cooling control
- Water cooling extruders
Return to
Consultants Corner