Many of the difficulties that screw designers encounter in trying to match extrusion theory to practice are due to the simplifying assumptions they make. One basic mistake is made whenever the drag flow equation is applied. This standard textbook equation is supposed to be useful in determining the pumping capacity of the extruder screw. It is often used in sizing equipment and in determining the proper channel depth needed to achieve the desired production rate.
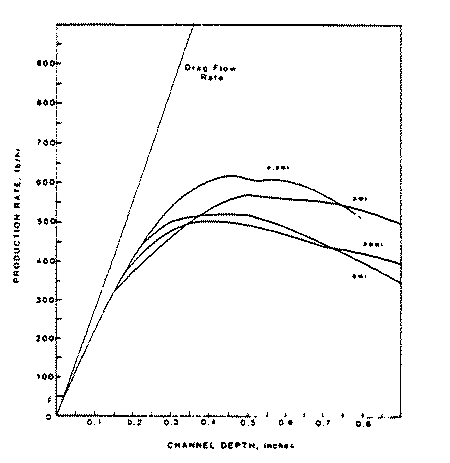
The drag flow equation, however, indicates that pumping capacity is proportional to channel depth as long as barrel diameter is constant. The designer, therefore, concludes from the equation that the deeper the channel, the higher the rate. The figure below shows production rate versus channel depth calculated from the drag flow equation alone (top line) for a 3½ inch diameter extruder processing LDPE at 80 rpm. The figure assumes that the metering section is 30 inches long, fed with a fully melted resin at 2000 psi with the extruder working with one particular die. According to this line, production rate increases by 280 lb/hr for every 0.1 inch increase in channel depth. Based upon this data, a designer might conclude that if an 8 M.I. LDPE were being processed at 500 lb/hr. an increase in depth of .05 inch would raise production rate to 640 lb/hr. In fact, the production rate would go up only to 525 lb/hr and the designer’s reputation would certainly not be enhanced.
The drag flow equation is not at fault here. The equation itself is quite correct, but it only tells half the story. A more sophisticated approach is required to accurately calculate the relationship between production rate and channel depth in melt pumping. For four different LDPEs shown, note that each material has an optimum depth. Shallower or deeper sections than the optimum can only result in lower production rates. Note also that for each material, the optimum is at different channel depth. Does this mean that the same screw cannot be used to process all four materials? No, only that there is a different best screw for each if production rate is used as the measure of screw quality. Of course, if extrudate temperature, power consumption and uniformity are also considered, then there is no single optimum screw. In such a case, each application demands different trade-offs and a screw that works well for one user may not be the best screw for another. But putting aside the criteria for an overall design for the moment, let us look only at production rate and deal qualitatively with the various effects which must be considered in determining optimum rate.
 22s.gif |
Production Rate Characteristic as a Function of Metering Section Depth in a 3 ½ inch Extruder Operating with Sheet Die. Four LDPE’s are Compared to the Drag Flow Rate.
Because the extruder is a centrifugal type pump, there are losses involved in its operation. In other words, a percentage of material pumped by the screw flows backward towards lower pressure areas nearer the feed. This is called backflow or pressure flow. The amount of backflow is determined by the head pressure, material viscosity and the depth of the extruder channel. When the backflow rate is added to the production rate, we arrive at the predicted drag flow. Therefore, determining the amount of backflow is the key to proper channel depth selection. By comparison calculation of drag flow in itself is relatively trivial and to a great extent, irrelevant. Because the backflow increases with in creased channel depth, we expect the true flow rate to diverge from the drag flow rate line and since backflow increases as viscosity drops, we also expect greater divergence for materials having a high melt index or low viscosity.
However, if the curves shown here are analyzed, we find that even this pattern is not maintained universally. Between depths of 0,400 and 0.500 inch, the curves fall pretty well in the expected pattern. At smaller depths, the 3 M.I. material has a lower production rate than expected and at greater depths, both the 2. M.I. and the 8 M.I. curves fall off disproportionately to the others.
To understand these results, we must take into consideration several additional facts, The major influence here is the temperature of the material. The higher the viscosity, the higher the viscous heat dissipation leading to a higher extrudate temperature, High temperature in turn reduces viscosity and so a steady state is reached. Because of this interaction, the rate at which viscosity falls with increased temperature and shear rate is actually more important to the final production rate than the nominal melt index, which is measured at one temperature and one shear rate.
It should also be noted that while the lower viscosity causes an increase in backflow, it also reduces die pressure which causes a reduction in backflow. In practice, this means that low pressure dies will deviate from the simple model much less than high pressure dies. In this case, our prediction is based on a sheet die with back pressure of 2,500-3,200 psi. Blown film dies, where pressure is higher would produce more strongly curving characteristics than those shown here.
Channel depth also influences the viscosity in a indirect manner as the deeper the channel, the lower the extrudate temperature becomes so long as flow rate continues to increase. This is because deeper channels shear the material less. However, lower temperature also causes an increase in die pressure by increasing the melt viscosity. Thus, the steady state is also effected by this interaction. Naturally, the shear rate is reduced in a deeper channel only so long as production rate increases. When production rate begins to drop, shear rate begins to rise, even though the channel may be deeper.
Thus, an accurate model of this system takes into account changes in the viscosity and cannot be based upon melt index or intrinsic viscosity alone. It also must deal with viscous heat generated in the screw channel and so isothermal equations will not serve. Finally, an analysis of the die is required as well as of the screw, as is knowledge of the heating and cooling capacity of the extruder barrel. Naturally, no single equation can be used to calculate all of the effects: Excellent correlation to reality can be achieved with the well developed non-Newtonian, non-isothermal models, but be cause of the many interactions involved, a careful evaluation of the entire process is a prerequisite to good design.
Given such a model, the next step becomes defining what is actually desired of the device. Overstating the die pressure requirements or temperature constraints can actually result in a worse screw for the task because the model may call for a shallower channel than actually required if the pressure is assumed to be high or for a deeper channel than optimum if low temperature is desired when it is not needed in the process. An understanding of these physical constraints is therefore important, even in the selection of proper design goals, let alone the design of a screw.
- Reuben Klein, Scientific Process & Research, Inc.
See also:
- Extensional viscosity and melt strength and their role in film blowing
- MD flow lines
- More on the drag flow equation
- Theoretical extrusion predictions
Return to
Consultants' Corner