Measurement of Diffusion Coefficients of Organic Volatile Components in Polymer Melts
C.D. Denson - Department of Chemical Engineering, University of Delaware, Newark, DE 19716
J. H. Frey and J. F. Nangeroni - Air Products and Chemicals, Inc., Allentown, PA 18195
INTRODUCTIONAccurate values of the binary polymer solvent diffusion coefficient of polymer melts are required for many processes involving the diffusion of a minor component solvent in a polymer matrix. These processes include the interphase mass transfer of a solvent from a polymer during polymer devolatilization, and the analysis of mixing in viscous polymer processing. Additionally, the understanding and prediction of reaction rates in reactive processing requires knowledge of the diffusion coefficient since mass transfer plays a major role in determining the extent of reaction in high viscosity systems undergoing laminar flow.
Unfortunately, only a few solvent/polymer systems have been studied extensively concerning the diffusion coefficient above the melting point of the polymer, and the diffusion data available to the polymer scientist are limited. Present techniques available to measure the diffusion coefficient of solvent/polymer systems above the polymer melting point are highly accurate, but they require a large investment in equipment and time. Consequently, most researchers and processors resort to either estimating a value of the diffusion coefficient based on data from similar systems, or treating the diffusion coefficient as an adjustable parameter. Denson (1983) points out that the later method can lead to values of the diffusion coefficient that are in sharp disagreement with actual values.
Most of the studies for diffusion in polymer melts have been performed with a sorption apparatus (Duda et al., 1973). Other methods for polymer melts involve free diffusion techniques where the concentration is measured as a function of position. Methods of measuring the concentration for free diffusion include interferometric techniques (Secor, 1967; Chalykh, 1983) and infrared absorbance (Klein and Briscoe, 1979). Another method used for diffusion of gases in polymer melts is the measurement of the pressure loss due to sorption (Lundberg et al., 1962).
We have developed a technique for measuring the diffusion coefficient of molten solvent/polymer systems that requires the use of equipment commonly found in the polymer analysis laboratory (Frey, 1987; Nangeroni, 1988). Furthermore, the time required to determine the value of a diffusion coefficient for many polymer systems at a single temperature is on the order of a day. The method used in this study is analogous to the quartz-spring sorption method (Duda et. a1. .1973), however, instead of a quartz-spring apparatus, a thermogravimetric balance (TGA) was used to measure weight loss. The TGA technique is strictly a desorption study, but it is conceivable to do a sorption experiment as well. The TGA technique is easier to use than most traditional polymer diffusion coefficient measurement methods, and a TGA balance ls available to most academic and industrial researchers.
THEORYMathematical methods for calculating the diffusion coefficient from sorption experiments on solvent/polymer systems with changing partial specific volumes have been described by Duda and Vrentas (1971) and Vrentas et al. (1977). In the present study, a simplified approach is taken in computing diffusion coefficients by assuming that partial specific volumes and diffusion coefficients are independent of concentration. Under these assumptions, the loss of solvent from a flat slab of polymer in the pan of a thermogravimetric balance is described by:
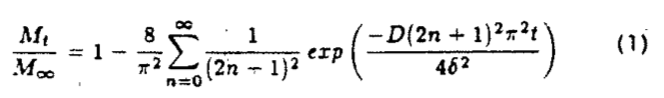
This equation, which is developed around the idea that the pan constitutes a no-flux surface and the gas phase contains no diffusant, can be solved to obtain approximate values for D
j (Crank, 1975) with an error of .001%. Thus:

and it is only necessary to know the half-time for weight loss and the slab thickness. When the diffusion coefficient is constant over a range of concentrations, the value of ( t/s
2)
1/2 is independent of M
oo the total amount of diffusant in the polymer.
If a solvent/polymer system does exhibit a strong solvent concentration effect on the diffusion coefficient, the technique provides an average diffusion coefficient over the concentration range of interest. Crank (1975) gives the definition of D
avg as:

Crank has further shown, by analysis of various forms of diffusion coefficient functionalities, that the average diffusion coefficient obtained from a desorption experiment ls equivalent to D
avg.
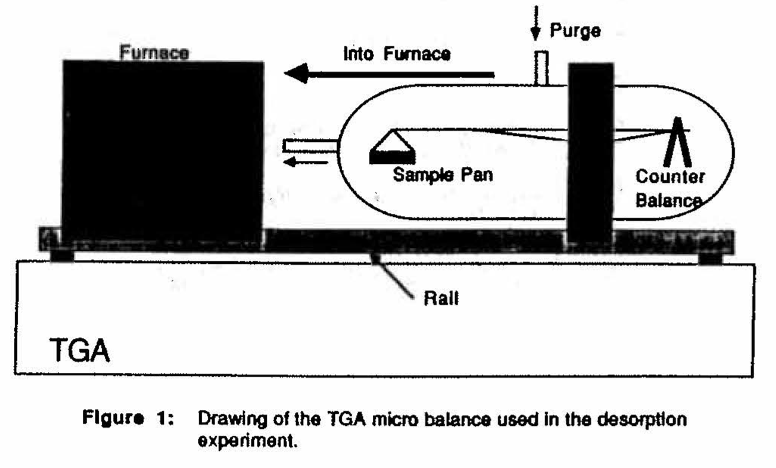
EXPERIMENTAL PROCEDURE AND MATERIALSA 950 Thermogravimetric Analysis balance made by DuPont was used to measure the weight loss from a polymer sample at elevated temperatures. A System 9900 computer made by DuPont was used to control the TGA and to record weight loss as a function of time from a polymer sample. The slab thickness was calculated from the melt density, sample mass, and sample pan diameter. The experimental micro-balance is shown in Figure 1.
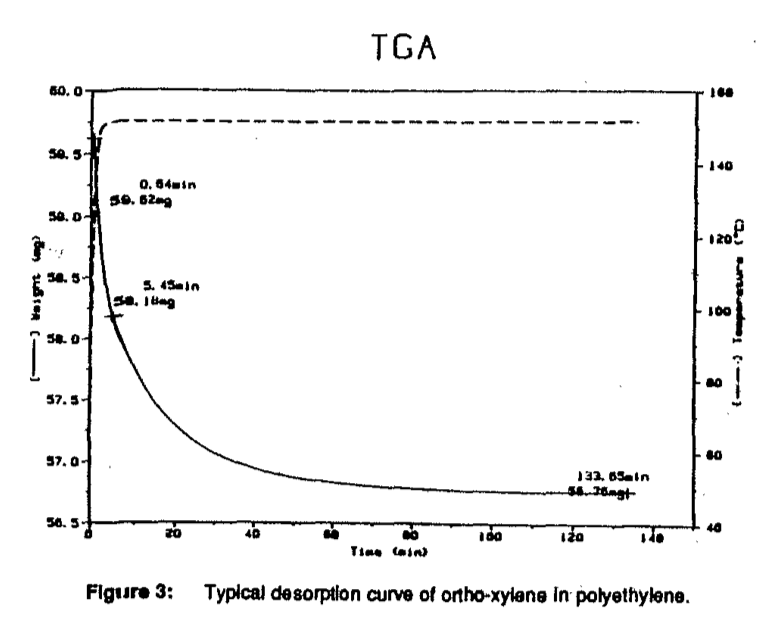
A solid polymer sample containing a specified concentration of a volatile component, cut roughly into a disk, was placed into a flat-bottomed sample pan and weighed. At time zero, the balance was carefully inserted into the high temperature furnace. The furnace was purged with an inert gas at a rate of 50 ml/min. Helium was used because the variation in density of the gas is negligible over the temperature ranges used in these experiments. Weight loss and temperature were monitored until a steady state was established. Two criteria determined the steady state: l) zero derivative of weight loss versus time and 2) sample weight loss equivalent to the theoretical weight loss. Typical experimental conditions used in the diffusion coefficient study are listed in Figure 2. A typical desorption curve for a sample of ortho-xylene in polyethylene is shown in Figure 3. The half-time was taken from the graph as the time required for the concentration of ortho-xylene to reach half of its initial concentration.
A lower flow-rate of stripping gas was used in one experiment to determine if there was a gas-phase resistance to the diffusing species. The lower purge rate did not significantly affect the diffusion coefficient.
The diffusion coefficient was calculated using an expression based on Equation (2) and using the half-time for weight loss determined from the TGA desorption curve. The slab thickness was written in terms of melt density, sample mass, and sample pan diameter.

The melt density was obtained on an Instron Capillary Rheometer. A plunger, moving at a constant velocity, displaced a known volume of molten polymer. The extrudate, collected over a known period of time, was weighed and a melt density computed.
The diffusion coefficients of five different solvent/polymer systems were measured using the TGA desorption technique. The accuracy of the method was determined initially by measuring the diffusion coefficient of ortho-xylene in polyethylene. Vrentas et al. (1982) measured the diffusion coefficient of ortho-xylene in polyethylene with a step change sorption apparatus. By comparing the results obtained by Vrentas with the TGA results, the accuracy of the technique could be verified.
Once the experimental procedure was verified, the diffusion coefficients of other solvent/polymer systems were measured. Figure 4 lists the polymer, molecular weight, solvent, and concentration ranges for all the systems investigated. The high molecular weight polyethylene was manufactured by DuPont under the trade name Alathon 2020. The low molecular weight polyethylene was manufactured by Eastman Chemicals and designated as Epolene Wax C-13. The Polystyrene was Mobil Chemical Polystyrene 1400.
Starting samples of the ortho-xylene/polyethylene and cyclohexane/polyethylene were prepared by wetting the polymer with solvent, and extruding the mixture through a 25 millimeter (mm) single screw extruder. The extruder melted the polymer and distributed the solvent. As the material exited the extruder, it was saved in sealed jars for subsequent analysis in the TGA. For the toluene/polystyrene system, the sample preparation technique was modified because of the strong solvating power of toluene in polystyrene. Instead of wetting the pellets of polystyrene wHh toluene, the toluene was injected under pressure into the extruder at a constant flow rate to form a concentrated solution of toluene in polystyrene. For the low molecular weight polyethylene samples, phthalic anhydride or para phenylene diamine were mixed into the polyethylene in a stainless steel resin kettle equipped with a lab motor and a stirrer. The resin kettle was heated in a 160°C oil bath and the mixture was stirred until a homogeneous sample was produced.
Results and Discussion
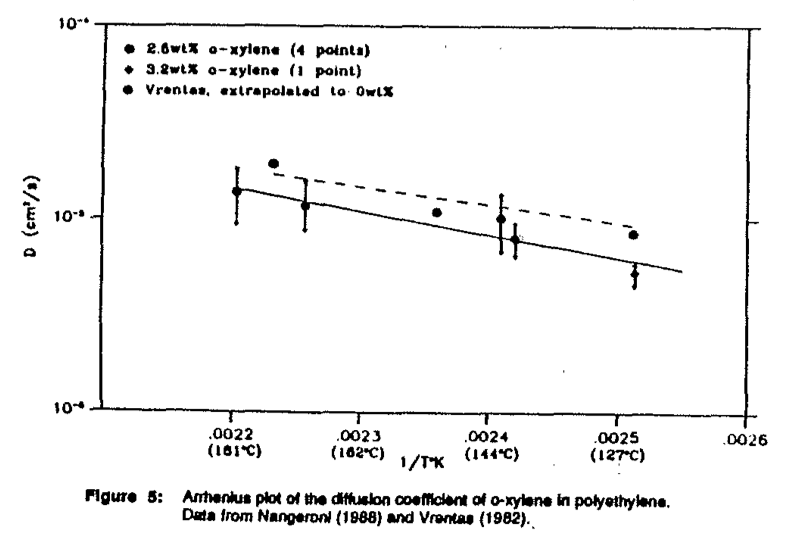
A series of experiments of the ortho-xylene/polyethylene system yielded values of diffusion coefficients that showed good agreement with the results obtained by Vrentas et al. (1982). An Arrhenius plot of the values obtained by Vrentas and values obtained in this investigation are shown in Figure 5. From this plot, the Arrhenius constants could be determined. These are listed in Figure 6 along with the Arrhenius constants obtained by Vrentas. The pre-exponential factor and activation energy for the Arrhenius expressions are slightly lower than those of the system used by Vrentas. This may be due to the differences in the polyethylene used in the two sets of experiments.
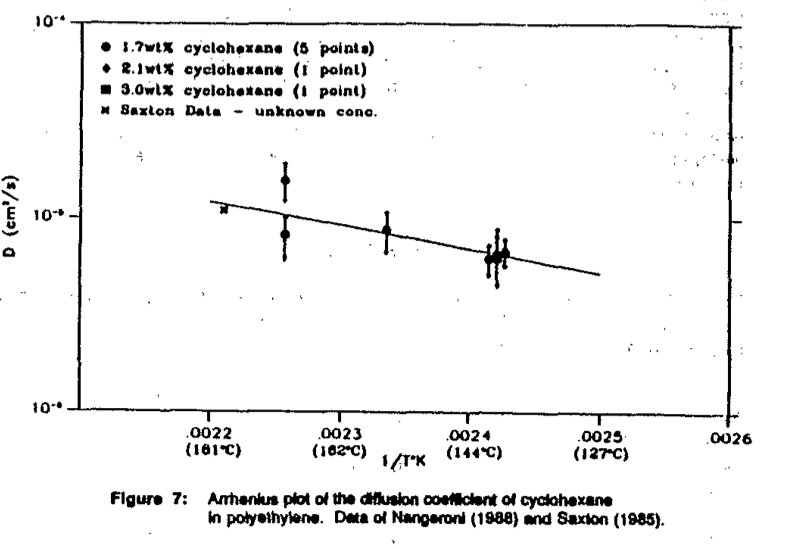
The TGA procedure proved to be an acceptable met.hod for determining the diffusion coefficients of volatile components in polymers, therefore, it could be used with confidence to predict values of the diffusion coefficients for other solvent/polymer systems. One application of the procedure was to determine the diffusion coefficient of cyclohexane in polyethylene for use in mass transfer studies in extensional flow fields (Nangeroni, 1988). Although diffusion data for similar compounds are available in the literature, an accurate value of the diffusion coefficient was required to reduce the experimental error in the analysis. The technique proved to be quite useful in determining the diffusion coefficients with an experimental error of +/- 20 percent. These results are presented in a Arrhenius plot in Figure 7. As with the a-xylene/polyethylene system, a negligible dependence of the diffusion coefficient with concentration was observed, therefore, the use of a constant diffusion coefficient in the analysis was appropriate. The Arrhenius constants are shown in Figure 6.
A second application of this technique arose during the analysis of micromixing in viscous polymers (Frey, 1987). The diffusion coefficients of chemical tracers in polyethylene wax were required. These systems did not have any published values, nor was there any similar system available from which a diffusion coefficient could be estimated. Values of the diffusion coefficients of phthalic anhydride in polyethylene and para-phenylene diamine in polyethylene were measured and Arrhenius expressions were developed. These are listed in Figure 6.
Finally, the diffusion coefficient of toluene in polystyrene was measured. Unlike the solvent/polyethylene systems, the diffusion coefficient of toluene in polystyrene was assumed to exhibit a strong dependence on concentration, since the temperature of interest was only slightly above the glass transition temperature (Tg) of polystyrene (llOOC). Polyethylene has a T
g of -123°C, which is well below the experimental temperature of 140°C.
The concentration dependence of the diffusion coefficient at the temperature ranges of interest has been shown by Duda et al. (i982) who obtained excellent agreement of experimental data and a modified free volume theory. Their model was useful for determining the average diffusion coefficient at temperatures and concentrations observed in polymer processing applications. The theoretical values based on the free volume theory of Duda can be calculated from:

where the subscript 1 indicates the volatile fraction and:
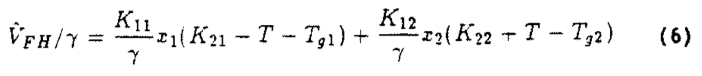
along with the expressions:
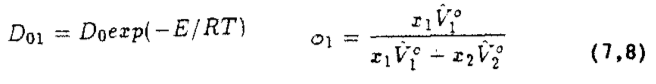
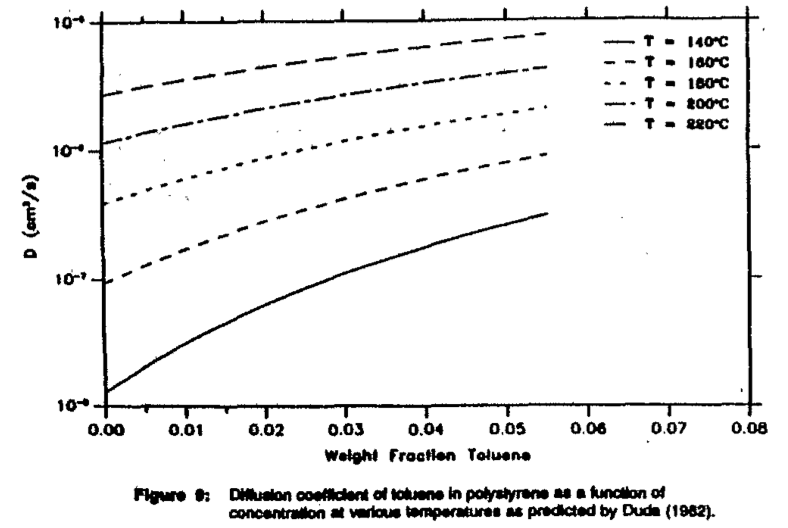
Values for the free volume parameters are given in Figure 8. Using Equation (5), the diffusion coefficients of toluene in polystyrene as a function of the concentration for various temperatures were calculated. Figure 9 shows the significant dependence of the diffusion coefficient with a changing concentration.
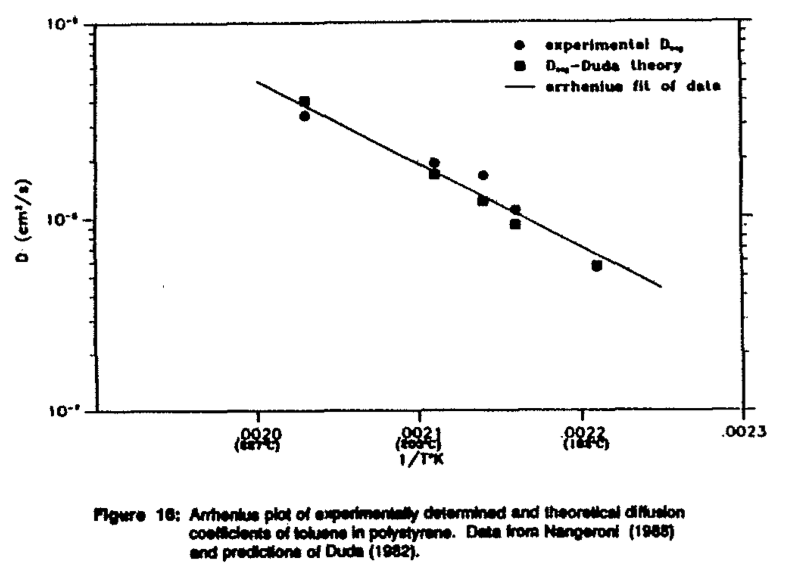
An Arrhenius plot of the average diffusion coefficients of toluene in polystyrene measured by the TGA desorption method is presented in Figure 10. An average diffusion coefficient based on the free volume theory can also be numerically calculated using Equation (5) in Equation (3). These values are also plotted in Figure 10. Excellent agreement is observed between the TGA results and the Duda model over a wide temperature range. This example demonstrates the usefulness of this technique for concentration dependent systems.
SummaryThe method for determining the diffusion coefficients of small organic molecules in a polymer by using a TGA was verified for organics in molten polymers. Experimental data were collected for five solvent/polymer systems. Excellent agreement was obtained between sorption data of Vrentas and TGA data for o-xylene in polyethylene. In addition, excellent agreement was obtained between experimental data of toluene in polystyrene and a modified free volume theory of Duda.
Certain cautions must be exercised in using this technique. First, the researcher must be aware of the geometry, boundary conditions, and physics involved in deriving the governing equations for the diffusion coefficient measurement. A flat slab of polymer, absent of bubbles, with an adequate inert gas purge must be employed in this experiment. Second, the analysis becomes slightly more complicated with a concentration dependent diffusion coefficient; however, diffusion coefficients can be obtained by performing several experiments at different concentrations. Finally, weight loss due to depolymerization must be identified by running a blank experiment with only polymer present. If these precautions are taken, the TGA diffusion coefficient measurement for polymer melt systems is a valid and accurate method of obtaining data for specialized systems encountered In polymer processing applications.
References

To view the original paper, please use the following link:
Best Paper 1989.pdfReturn to
Best Papers.