A Mechanism for Solid Bed Breakup in Single-Screw Extruders
Gregory A. Campbell, Clarkson University/Castle Associates, Jonesport, ME
Mark A. Spalding, The Dow Chemical Company, Midland, MIAbstract
Solid bed breakup in plasticating single-screw
extruders can lead to defects in the downstream product,
reduced rates, and process instabilities. The literature
generally attributes this breakup to pressure gradients
emanating from the beginning of the metering section of
the screw although little evidence is available. In this paper
a new mechanism is proposed that was developed as a
result the melting mechanism and fluid flows associated
with screw rotation physics.
Introduction
Solid bed breakup is a process that occurs in almost all
plasticating single-screw extruders, and in most cases the
process is undesirable since it can lead to solid polymer
fragments in the extrudate, process instabilities due to
solids plugging mixers, and thermal gradients [1]. Solid
fragments in the extrudate will almost always cause defects
in the finished product. For example, a lab extruder was
operated with a mixture of 100 parts of white tinted
acrylonitile-butadiene-styrene (ABS) terpolymer pellets
with 1 part of black tinted ABS pellets. If the extruder
operates properly without solid bed breakup, the extrudates
are tinted black and are relatively uniform in color, as
indicated by the cross sections shown in Figure 1 at screw
speeds less than about 70 rpm. At higher screw speeds, the
solid bed broke up and caused solid polymer fragments to
flow downstream and into the extrudate, as indicated by
the white tinted fragments at screw speeds greater than 80
rpm.

Figure 1. Cross-sectional views of extrudate samples at a letdown ratio of 100 to 1 of a white pigmented ABS resin with a black color concentrate for a melting-mixing experiment.
Solid bed breakup can be observed by performing a
Maddock solidification experiment [2], as indicated by the
photographs in Figure 2. Here the black tinted areas show regions in the screw channels that were molten at the
moment of stopping screw rotation and solidifying the
resin. Areas that were tinted white show regions that
contain resin in the solid form. Solid bed breakup is
evident in these cross sectional photographs since there are
regions were the molten resin is essentially across the
entire channel and solids are evident in downstream cross
sections. These types of views are typical in almost all
published Maddock solidification experiments.
Literature references discuss solid bed breakup as a
phenomenon where strong forces due to pressure gradients
breakup the low strength solid bed [3,4]. The source of the
pressure gradients, however, is not evident. Zhu et al.
constructed an extruder with glass windows for viewing
the internal processes during extrusion [5] and injection
molding [6]. Their observations indicated that solid bed
breakup was more likely to occur at high screw speeds,
consistent with the observations discussed previously. For
injection molding plasticators, bed breakup is more likely
to occur for long injection strokes, high discharge pressure
(back pressure), and long dwell times. They observed small
cracks that occurred across the solid bed and perpendicular
to the flights in the later stages of the melting process.
These cracks would then increase in width as they were
filled with molten polymer. Their observations are
consistent with previous researchers. The mechanism for
the crack formation was not reported.
The current melting and conveying mechanisms using
barrel rotation physics do not provide an explanation for
solid bed breakup. Screw rotation physics, however,
provides a melting mechanism and a flow mechanism that
explains the solid bed breakup process in single-screw
extruders. This is the first time that a mechanism has been
proposed for solid bed breakup that fits the observed data.
Melting Mechanism Literature
The key to understanding solid bed breakup is the
comprehension of the melting mechanism that occurs in
the extruder using the actual boundary conditions for screw
rotation physics. This melting mechanism will be outlined
in this section.
Recently the Polymer Processing Research group at
Clarkson University reexamined the melting data published
in Tadmor and Klein [3] and found that in essentially all
cases the material in a conventional screw transition
section disappeared in the height direction before the width
direction, as shown in the reanalysis of the data in Figure 3. This was in direct contrast from the melting theory
developed by Maddock [2] and the model developed by
Tadmor and Klein [3]. The Tadmor and Klein model had
the solid bed disappearing in the width direction only.
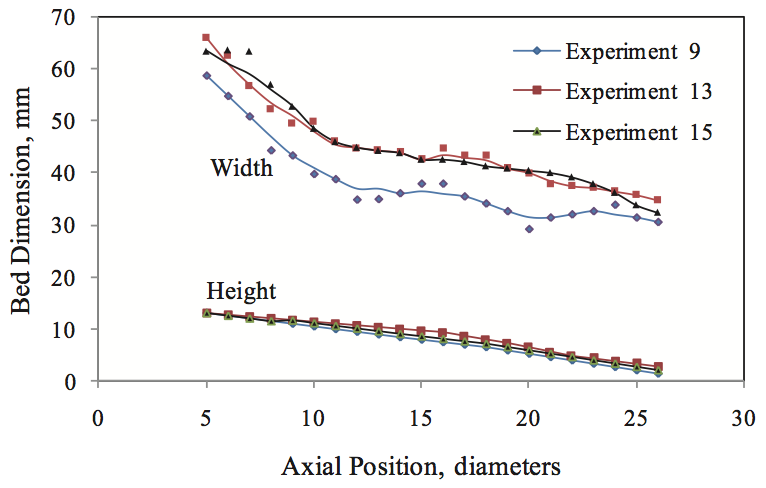
Figure 3. Reevaluation of the melting data from Tadmor and Klein for PE resins [3] as analyzed by Tang [7] and Campbell et al. [8,9].
Earlier literature, using barrel rotation boundary
conditions, was developed that addressed the effect of the
film under the solid bed on its movement and breakup:
they include the effect of the melt film on the solid bed
velocity [10,11]; the effect of the melt film on bed
acceleration, [12,13,14]; and the use of striations to
determine local bed velocity [15]. Lindt and his research
group investigated and reported a body of work for a series
of complete mathematical models for the melting process.
Lindt [16] developed a model by considering the solid bed
in the center of the cross-section in 1976 using barrel
rotation theory. Lindt focused his later work on the fivezone
melting model [17-20]. Lindt, Elbirli, Gottgetreu, and
Baba [17] developed a model by considering all zones of
the channel that previous people considered separately.
Lindt and Elbirli [18] considered the cross section
circulation in the model in 1985 where the screw was still
considered to be stationary. Also in 1985, Lindt claimed
that “the development of the melting theory based on the
Maddock Mechanism has been virtually completed [19].”
A new melting mechanism was developed using screw
rotation physics that is diagrammatically portrayed in
Figure 4. The rotation of the screw creates a velocity
gradient at the barrel-solid bed interface and the
combination of the heat flux from the barrel and the
dissipation in Film C cause the solid to melt in the negative
y direction. The motion of the screw under the bed
contributes to the energy dissipation in Film D, causing the
bed to melt in the positive y direction. The same
mechanisms occur in Zones E and B to melt the solid bed in the x directions. A major difference in this mechanism
compared to the historic literature analysis is that the bed
does not reorganize.
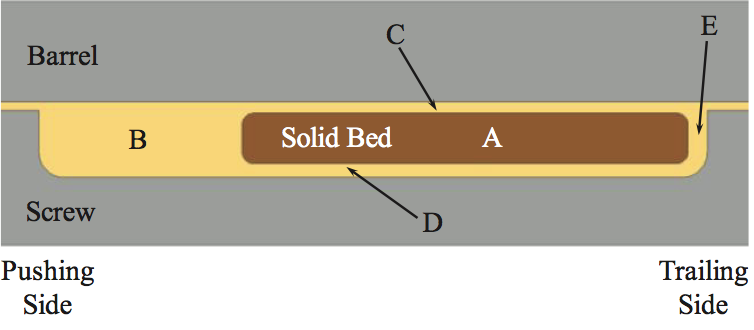
Figure 4. Schematic for the zones of the new melting concept: Zone B is the melt pool, Zone C is the melt film located between the solid bed and the barrel wall, Zone D is the melt film between the solid bed and the screw root, and Zone E is the melt film between the solid bed and the trailing flight. The cream color represents molten resin.
The Tadmor and Klein model [3] allows melting only
in the Zone C film located between the solid bed and the
barrel wall, as shown in Figure 4. The material melted is
then dragged by the motion of the barrel and collected in
the melt pool of Zone B. As melting progresses, the melt
pool increases in width and the solid bed decreases in
width. The solid bed is assumed to reorganize such that it
covers the full depth of the channel. Near the end of
melting, the Tadmor melting model and other literature
models have the last remaining portion of the solid bed
positioned at the trailing flight and across the full depth of
the channel, as shown by Figure 5a. These models are all
based on barrel rotation physics.
As previously mentioned, the Tadmor and Klein
model forces all melting to occur in Zone C. The melting
that occurs at the other zone interfaces with the solid bed is
ignored because the velocity gradients and thus energy
dissipations were believed to be very small. These
gradients are due to the solid bed moving at a velocity V
sz
calculated from a mass balance at the entry to the melting
section and a stationary screw; i.e., barrel rotation physics.
Recently Campbell, Spalding, and Tang [21,22] have
reexamined the assumptions in the literature models in
order to address the reanalysis of the classical melting data
discussed previously and as shown in Figure 3. This
concept was developed based on recognizing that the rate
limiting melting dynamics for solid bed consumption was
in the channel height direction and not the channel width
direction. Here the melting process occurs in all four of the
melt films surrounding the solid bed, as shown in Figure 4.
The boundary conditions were set to those for screw
rotation physics.
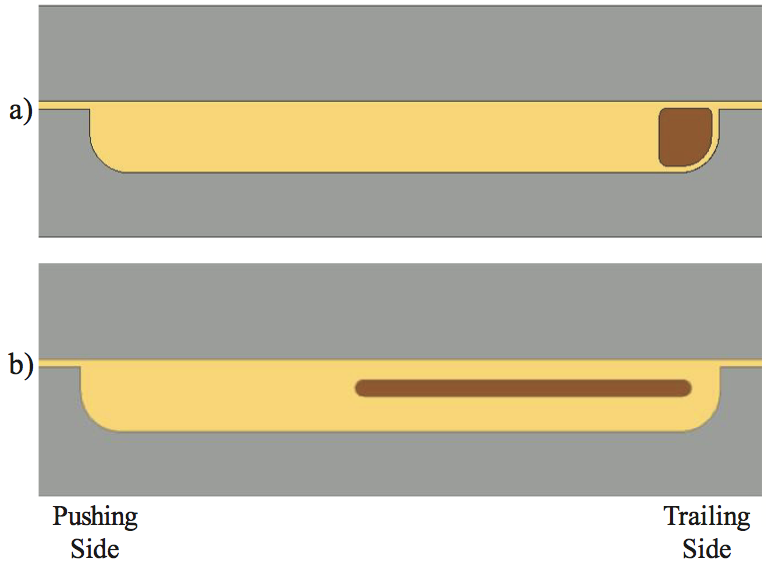
Figure 5. Schematics of the solid bed just prior to complete melting: a) the solid bed is pushed to the trailing flight with the Tadmor melting model and barrel rotation physics, and b) the solid bed is a thin plate and positioned as in the diagram (screw rotation and observation). The cream color represents molten resin.
To visualize the difference between screw rotation and
barrel rotation, a simple cardboard paper towel roller can
be used to model the screw core and a wood block to
model the solid plug. For barrel rotation, the roller is held
constant and the block is moved downstream at a velocity
of V
sz. Here the velocity difference between the block and
roller is simply V
sz. For screw rotation, the roller is rotated
counterclockwise while the block is moved downstream
with a velocity of V
sz. The observer will see that the core of
the screw is moving in the negative z (helical) direction at
a velocity of V
cz. The velocity difference for Zone D is as
follows:
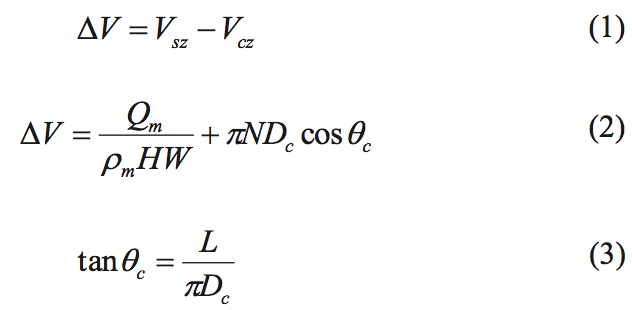
where ΔV is the velocity difference between the solid bed
and the root of the screw, Q
m is the mass flow rate, ρ
m is
the bulk density of the solids at the start of melting, H is
the channel depth at the start of melting, W is the average
channel width, N is the rotation rate of the screw (rev/s), D
c
is the diameter of the screw at the root (or core), ϴ
c is the
helix angle at the screw root, and L is the lead length. The
first term on the right side of Eq. (2) is V
sz while the second
term is –V
cz. A schematic of the velocity difference is provided in Figure 7. This velocity difference is
considerably larger than that for barrel rotation physics.
The screw rotation model here includes the dissipation and
melting rates for all zones.
Developing a physical model for these melt zones,
leads to a description of the flow dynamics in the films that
exist in the screw channel from the beginning of the
melting of the solid bed through the transition section that
ends at the beginning of the metering section. A schematic
of a typical solid bed profile is provided in Figure 6 with
the solids profile near the end of melting shown in Figure
5b for screw rotation. The fluid velocity gradient in Film C
at the top of the solid bed is in the x direction which causes
fluid to be deposited into Zone B. The fluid velocity in
Film D between the screw root and the solid bed in Figure
4 is a more complex recirculation flow due to motion of
the screw surface in the opposite direction of the solid bed.
That is, the screw root motion drags fluid into the Film D
gap at the end of the transition section. Some of the fluid
that is dragged into Film D is thought to flow into Zone B
due to a higher pressure under the solid bed than in the
melt pool (Zone B). This pressure under the solid bed is a
key to the mechanism for solid bed breakup.
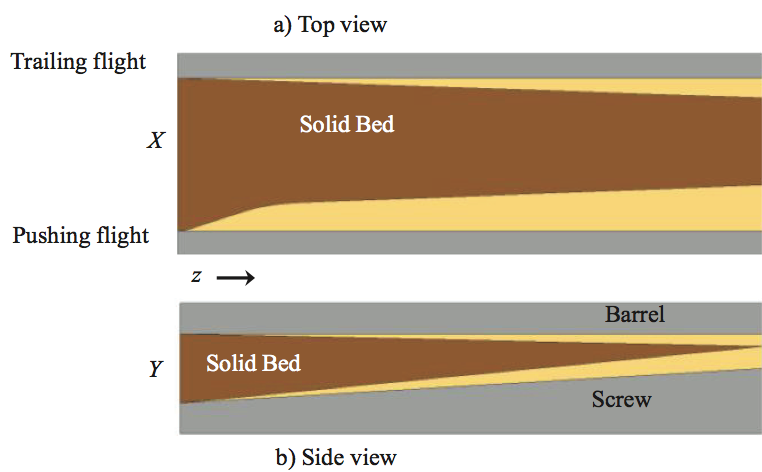
Figure 6. Qualitative shape of X and Y bed dimensions and melt film thickness for melting in a conventional transition section; a) top view, and b) side view. The cream color represents molten resin. Here X and Y are the local width and thickness of the solid bed, respectively.
The melting mechanisms described earlier for a
conventional transition section assumes that the solid bed
remains continuous throughout the entire melting process.
For most extrusion processes, however, this is not the case.
Instead the solid bed can breakup near the completion of
melting, that is in the transition as it approaches the
metering section. At this point in the melting process the
bed is relatively thin and its cohesive strength is low. The
strength of the bed is low at this location since the solid
bed temperature is approaching the melting temperature or devitrification temperature and thus the material modulus
is low. Because the bed is thin in the y direction there is
little stability. Evidence of solid bed breakup is apparent in
photographs of Figure 2. Moreover, solid bed breakup is
evident in almost all reported Maddock solidification
experiments for a conventional melting screw.
The Mechanism for Solid Bed Breakup
As will be presented next, two processes are required
for solid bed breakup. These processes include the melting
mechanism presented above for screw rotation physics and
a flow mechanism for transporting molten resin between
the solid bed and the screw root (the flow in Film D).
It is obvious that the strength of the solid bed would be
low near the end of melting since the bed is very thin and
its temperature is approaching the melting or
devitrification temperature. Based on the historical melting
models using barrel rotation physics, the pressure gradients
postulated for breaking the bed are difficult to produce. In
general, the pressure gradient in the transition section is
positive such that one might speculate that this would
stabilize the bed by pushing the solids back toward the
thicker and more stable portion of the bed. However, screw
rotation theory leads to an alternative mechanism to those
based on barrel rotation theory. Screw rotation theory is
presented in great detail in [1,23-27] for the metering
section. For screw rotation analysis, the barrel has zero
velocity and the solid bed is moving in the positive z
direction at a velocity of V
sz. The screw has a velocity of
–V
c and a component in the z direction of -Vcz. Here, the
backward motion of the screw (ǀ-V
czǀ or V
cz) is larger than
V
sz, causing a negative pressure gradient (∂P/∂z) in Film D
between the solid bed and the screw root.
The locally higher pressure underneath the solid bed in
Film D of Figure 7 is postulated to exist and force the solid
bed up against the barrel surface, this would be consistent
with the observation that the solid bed is always near the
barrel surface with only a thin film of fluid between the
barrel and the solid bed. There can be a substantial
thickness of melt in Zone D. The pressure in Film C has
been experimentally measured by many researchers. The
local pressure in Film C is always less than the pressure in
the melt pool. With the local pressure in Film C being less
than that in the melt pool and with the pressure in Film D
higher than the melt pool, it follows that difference in the
pressures create a force the pushes the solid bed against the
barrel wall.
The locally high pressure underneath the solid bed and
the positive ∂P/∂x in Film D causes some flow of resin
from Film D to the melt pool (the x origin is on the pushing
flight). Thus, for a local Δz increment for Film D, there is
material entering the element from the melting process and from the drag motion of the screw core, and there is
material leaving the increment from the motion of the
screw core and from the flow of material into the melt pool
due to a positive ∂P/∂x. These complex flows are
consistent with observations from Maddock solidification
experiments. This flow is shown in detail for the Maddock
solidification experiment shown in Figure 8.
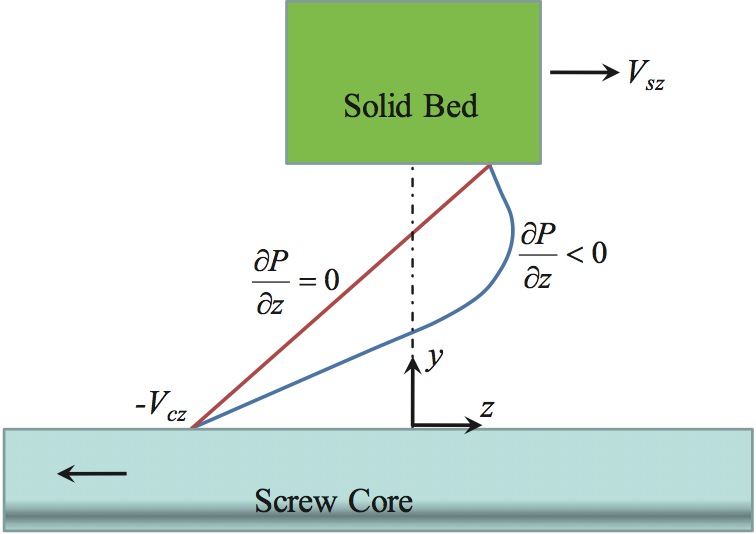
Figure 7. Schematic of the Vz velocity in the Film D between the screw core and the solid bed. The red and blue velocity lines are for pressure gradients that are zero and negative, respectively. The dotted vertical line is for Vz = 0

Figure 8 Photograph of resin solidified in the transition section after a Maddock solidification experiment for an ABS resin: a) the arrow is pointing at the flow lines created by the flow of material from Film D out to the melt pool, and b) an enlargement of the flow area.
The flow from the film between the solid bed and the
screw root (Film D) can be observed in most Maddock
solidification experiments, as shown in Figure 8. The
section in this photograph was for a location early in the
melting process where the strength of the solid bed is high
and can withstand the pressure gradient created by the flow induced by the backwards motion of the screw. The high
strength of the bed prevents the bed from breaking up.
Flow lines due to poor mixing of the colorant into the
white resin show the flow from Film D into the melt pool.
The flow is substantial as it is pushing and deforming the
recirculating flow of the pool away from the solid bed.
These flow patterns can be observed in Figure 2 with
careful observation, and the observed flow pattern is not
consistent with a barrel rotation model.
The expected velocities and pressure gradient are
shown in Figure 7. That is, the backwards motion of the
screw is dragging molten polymer backwards at the screw
root and generating a significant level of pressure in Film
D. When the strength of the solid bed is relatively high, the
high pressure in Film D causes material to flow out to the
melt pool B. If the strength of the solid bed is relatively
low, then the bed will form a small crack due to the fluid
flow induced stresses at the bottom interface of the solid
bed, and then the crack will then fill with fluid as observed
by Zhu et al. [5,6]. Since the screw core develops
predominately recirculating flow under the bed, then fluid
would be expected to also flow under the solid bed toward
the metering section (see blue line in Figure 7). This
recirculating flow would cause a shear stress on the bottom
of the solid bed. The upstream velocity in conjunction with
the bed low cohesive energy and cracks would tend to
cause fragments to break off of the bed. The surface shear
stress from the recirculating fluid would thus drag the solid
bed fragments away from the solid bed and into the
metering section. The solid bed breakup process is
qualitatively described in Figure 9.
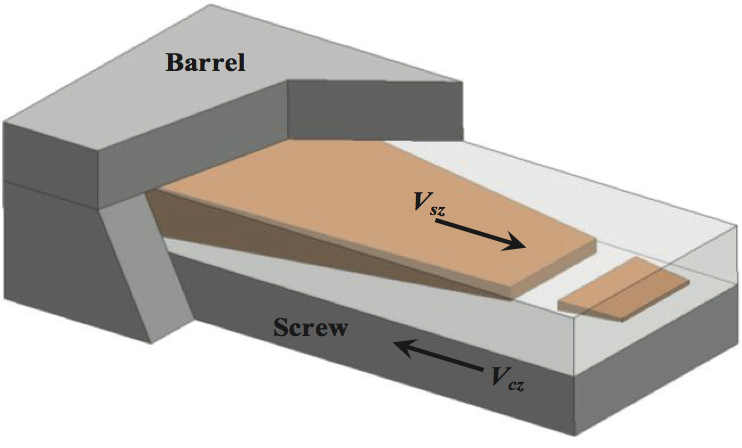
Figure 9. Schematic for solid bed breakup.
Figure 9 qualitatively describes the solid bed breakup
process. For this process, the solid is moving in the V
sz
direction. The motion of the screw drags fluid into Film D
between the screw root and solid bed, creating a relatively
high pressure in the film. When the strength of the solid
bed is high, the high pressure induces flow out of the film into the melt pool. The flow out of Film D into the melt
pool is observed in Figure 8. When the strength of the solid
bed becomes low near the end of the melting process, the
pressure produces a crack as shown in Figure 9, and then
the crack fills with fluid as observed by Zhu et al. [5,6].
Discussion
The melting model based on screw rotation physics
and the flow due to the negative V
cz velocity provides the
mechanism for solid bed breakup. This is the first time that
solid bed breakup has been explained mechanistically.
Barrel rotation physics and models have been unable to
explain adequately solid bed breakup. The mechanism
provided here is consistent with flows observed during
Maddock solidification experiments and the observations
by Zhu et al. [5,6].
The recirculating flow in the melt pool and the flow
entering the pool from Film D create a region at the screw
root where the flows are likely very low or form eddies.
This low flow region where the recirculating and entering
flow merge is shown in Figure 10. For most extrusion
processes, this low flow region is not a problem and likely
very difficult to detect. For thermally sensitive materials
such as polyvinylidene chloride (PVDC) resin, the long
residence time of the region can cause a ribbon of degraded
material to form on the root of the screw where the flows
merge. This ribbon typically starts when the melt pool first
forms and ends when the melting process is about 70%
complete. A photograph of this type of degradation is
shown in Figure 11. Processing changes can mitigate this
type of degradation [28].
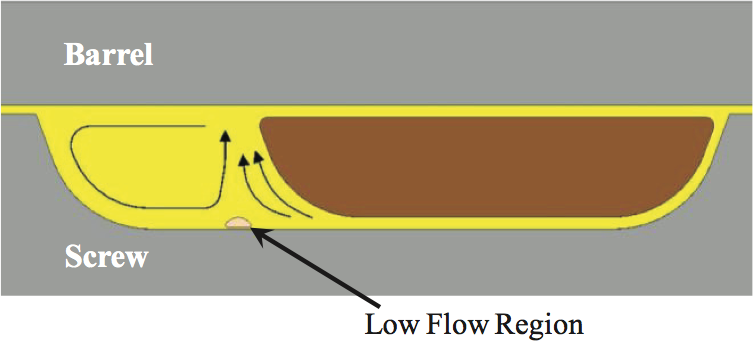
Figure 10. Schematic showing the recirculating flow in the melt pool and the flow entering the melt pool from Film D.
A low flow region exists where the flow streams merge.
The degradation ribbon at the merge of the flows
occurs because of the low flow region created between
cross channel flow of material from Zone D and the
recirculation flow in the melt pool. As shown by Figure 8,
this flow from Zone D is relatively large. As previously
stated, the flow occurs because of pressure induced flow
and the dragging of fresh material under the solid bed by
the backwards motion of the screw root. This process is
consistent with the physics presented for screw rotation.
The flow fields developed for a barrel rotation system
would not create the low flow region such as shown in
Figure 11.

Figure 11. Photograph of a segment from a Maddock solidification experiment for a PVDC resin extrusion. The dark band is degraded resin due to a long residence time at the location.
For processes with relatively low compression rates
such that the air entrained between the pellets is not readily
pushed back out the hopper, solid bed breakup will
eliminate a pathway back to the hopper. In this case the
entrained air will discharge with the extrudate and often
create defects in the product.
Solid bed breakup can be mitigated using screw design
and process conditions for a conventional screw design.
For example, the largest single contributor to bed breakup
is high screw speeds. For a particular screw, the extrudates
were relatively free of solid polymer fragments at low
screw speeds. But at screw speeds above about 75 rpm,
solid bed breakup is occurring and high levels of solids are
discharged with the extrudates. Although not desirable for
a commercial process, decreasing the rate of the line is
often a short term fix for eliminating solids in the
discharge. Placing a finer screen in the screen pack is also
an acceptable short term remedy. The best long term fix is
to add an acceptable dispersive mixer to the screw or to
install a high-performance screw.
Several high-performance screws actually take
advantage of solid bed breakup by using the small solid
fragments as a cooling method for the extrudate. For these
designs, the solid polymer fragments are reduced in size
using dispersive type dams. The small fragments are then
melted primarily by heat conduction from the hot molten resin to the cooler solid fragments, decreasing the
temperature of the molten stream. Common commercially
available high-performance screws that employ this
technology include Wave screws [29,30], Energy Transfer
screws [31,32], Fusion screws [33], and DM2 screws [34].
Summary
The process of solid bed breakup is described and
demonstrated using photographs from Maddock
solidification experiments. A new theoretical hypothesis is
developed based on screw rotation theory that proposes
that the bed breakup is due to the melting process and the
backward flow of material under the solid bed, creating a
high pressure in this gap. If this pressure is high enough to
break the solid bed, solid bed breakup will occur.
Acknowledgements
The authors are grateful to many colleagues and
students that worked to develop these techniques.
References
1. G.A. Campbell and M.A. Spalding, “Analyzing and
Troubleshooting Single-Screw Extruders,” Hanser
Publications, 2013.
2. B.H. Maddock, SPE J., 15, 383 (1959).
3. Z. Tadmor and I. Klein, “Engineering Principles of
Plasticating Extrusion,” Van Nostrand Reinhold
Company, New York, 1970.
4. C.I. Chung, “Extrusion of Polymers, Theory and
Practice,” second edition, Hanser, Munich, 2011.
5. F. Zhu, A.C.-Y. Wong, R. Liu, and T. Liu, Plastics,
Rubber and Composites Processing and Applications,
26, 8, 343 (1997).
6. Z. Jin, F. Gao, and F. Zhu, Polym. Eng. Sci., 44, 1313
(2004).
7. Z. Tang, MS Thesis, Clarkson University, Potsdam,
NY, Chemical Engineering Department (1999).
8. G.A. Campbell, Z. Tang, C. Wang, and M.
Bullwinkel, SPE-ANTEC Tech. Papers, 49, 213
(2003).
9. G.A. Campbell and Z. Tang, SPE-ANTEC Tech.
Papers, 50, 162 (2004).
10. R.C. Donovan, Polym. Eng. Sci., 11, 484 (1971).
11. R.C. Donovan, SPE-ANTEC Tech. Papers, 16, 561
(1970).
12. J.R. Edmondson and R.T. Fenner, Polymer, 16, 49
(1975).
13. R.T. Fenner, A.D.P. Cox, and D.P. Isherwood, SPEANTEC
Tech. Papers, 24, 494 (1978).
14. J. Shapiro, A.L. Halmos, and J.R.A. Pearson, Polymer,
17, 905 (1976).
15. H. Fukase, T. Kunio, S. Shinya, and A. Nomura,
Polym. Eng. Sci., 22, 578 (1982).
16. J.T. Lindt, Polym. Eng. Sci., 16, 284 (1976).
17. B. Elbirli, J.T. Lindt, S.R. Gottgetreu, and S.M. Baba,
Polym. Eng. Sci., 24, 988 (1984).
18. L.T. Lindt and B. Elbirli, Polym. Eng. Sci., 25, 412
(1985).
19. J.T. Lindt, Polym. Eng. Sci., 25, 585 (1985).
20. J.T. Lindt, Polym. Eng. Sci., 21, 1162 (1981).
21. G.A. Campbell, M.A. Spalding, and Z. Tang, SPEANTEC
Tech. Papers, 55, 147 (2009).
22. G.A. Campbell and M.A. Spalding, SPE-ANTEC
Tech. Papers, 56, 418 (2010).
23. G.A. Campbell, P.A. Sweeney, and J.N. Felton,
Polym. Eng. Sci., 32, 1765 (1992).
24. G.A. Campbell, P.A. Sweeney, and J.N. Felton, Int.
Polym. Proc., 7, 320 (1992).
25. G.A. Campbell, P.A. Sweeney, N. Dontula, and C.
Wang, Int. Polym. Proc., 11, 199 (1996).
26. G.A. Campbell, H. Cheng, C. Wang, M. Bullwinkel,
and M.A. te-Riele, SPE-ANTEC Tech. Papers, 47, 152
(2001).
27. G.A. Campbell, C. Wang, H. Cheng, M. Bullwinkel,
and M.A. te-Riele, Int. Polym. Proc., 16, 323 (2001).
28. S.R. Jenkins, J.R. Powers, K.S. Hyun, and J.A.
Naumovitz, J. Plast. Film & Sheet, 6, 90 (1990).
29. G.A. Kruder, US Patent 4,173,417 (1979).
30. G.A. Kruder and W.N. Calland, SPE-ANTEC Tech.
Papers, 36, 74 (1990).
31. C.I. Chung and R.A. Barr, U.S. Patent 4,405,239
(1983).
32. C.I. Chung and R.A. Barr, SPE-ANTEC Tech. Papers,
29, 168 (1983).
33. T.W. Womer, E.J. Buck, and B.J. Hudak Jr., US
Patent 6,672,753 (2004).
34. M.A. Spalding, J.A. Kuhman, D. Larson, J. Kuhman,
and H.L. Prettyman, SPE-ANTEC Tech. Papers, 50,
599 (2004).
35. M.A. Spalding and G.A. Campbell, SPE-ANTEC
Tech. Papers, 55, 1174 (2009).

Figure 2. Melting profiles for a 63.5 mm diameter extruder running an ABS resin at 60 rpm for screws with a 3.18 mm deep metering channel, 6 diameters of feed section, 8 diameters of transition, and 7 diameters of metering section: a) compression ratio of 2.0, b) compression ratio of 2.4, c) compression ratio of 2.8, and d) compression ratio of 3.2 [1]. The pushing flights are on the right side of the section photographs. The void marks on c) at diameters 16 through 20 were caused by the resin shrinking slightly as it cooled. Compression ratio (C) and compression rate (R) defined in reference [35].
Return to
Paper of the Month.