Prediction of Secondary Flows in Non-Circular Ducts Using the Radial Functions Method
Iván D. López
(1,2), Lori T. Holmes
(1) and Tim A. Osswald
(1)
(1) Polymer Engineering Center, University of Wisconsin-Madison
(2) Plastic and Rubber Institute (ICIPC), Medellin-Colombia
Abstract
The flow through non-circular tubes is simulated
using the radial functions method (RFM). The Giesekus
model is considered to reproduce viscoelastic effects.
RFM is a meshless technique that does not require
homogeneous grid points. The technique successfully
modeled the flow through square tubes reproducing the
secondary flows observed experimentally by other
researchers. Furthermore, the results are in agreement
with finite element and finite volume numerical
approaches. When considering high Weissenberg
numbers, meshless techniques avoid the limitations of
typical methods using meshes, such as capturing steep
stress gradients at sudden changes in geometry.
Introduction
For two decades, researchers have been working on
the modeling of viscoelastic flows in 3D geometries.
Although some complex flows have been successfully
simulated, they are still limited to low Weissenberg
number (We) values while requiring high computational
times. Meshless techniques such as the Radial Functions
Method (RFM) offer a novel and an interesting approach
to study viscoelasticity. In particular, this work is focused
on the prediction of secondary flows caused by
viscoelastic effects in straight non-circular ducts, which
are typical in geometries of extrusion dies.
The magnitude of the secondary flows is usually
many orders lower than the axial flow. However, they
may produce significant impacts in practical applications.
Syrjala [15] demonstrates using the finite element method
that secondary flows can affect drastically the temperature
distribution in low-viscous flows. Dooley [3,4]
investigates how the presence of secondary flows
generates elastic layer rearrangement in multilayer
coextrusion, which results in layer thickness variations.
Yue et al. [17] summarize the publications that have
reported results of simulations of secondary flows in
noncircular ducts. Those publications include the work of
Debbaut [2] and Dooley [3,4] using the Giesekus model with finite elements, and the work of Tanoue et al. [16]
predicting secondary flows with the PTT model.
Experimentally, several authors have observed
recirculations in elliptic pipes [6] and square cross-section
ducts [3,4].
Only in the last six years the applications of meshless
techniques with radial basis functions have been extended
to the simulation of non-Newtonian flows. Those works
includes the publications of Er-Riani et al. [5], López,
Osswald et al. [8-11,13], Mai-Dui and Tanner [12],
Bernal and Kindelan [1]. The viscoelastic study with
radial basis functions is reduced to the work of Mai-Dui
and Tanner [12], who simulated the axisymmetric flow in
tubes using Newtonian, power-law, and Oldroyd-B
models and flows through straight ducts using the
Criminale–Ericksen–Filbey (CEF) model with a stream
and vorticity approach. That work represents an
important step in the solution of viscoelastic flows using
meshfree methods. However, the solution of a CEF model
does not guarantee the solution of more complex models
such as Phan Thien Tanner (PTT) and Giesekus models,
and the stream and vorticity approach may not work for
three-dimensional solutions. In the present work, the
solution with RFM is formulated for a general differential
constitutive equation, using in particular the Giesekus
model, and compared with results observed
experimentally and solved numerically by other
researchers.
Modeling and Numerical Implementation¶
The secondary flows of viscoelastic fluids in
noncircular straight ducts are orthogonal to the main
direction of the flow. They are caused by the stress tensor
components in the transverse plan. The duct geometry
plays an important role in the generation of recirculations,
wherefore secondary flows are only formed in non-axissymmetric
cross-sections . A detailed description of the
mechanisms that generate secondary flows is presented by
Yue et al. [17].
In order to model viscoelasticity, the stress, τ, is split
into a purely viscous component, τ
N, and an extra-stress,
τ
v which contains the elastic components. This stress split has an important impact on the numerical stability of
the governing equations [14]. The total stress can be
written as

Neglecting inertia and gravitational effects, the
momentum equation can be written as,

The constitutive equation for τ
N is given by

where
s is a weight factor between 0 and 1 that indicates
how important is the Newtonian contribution of the stress
compared to the total stress.
The viscoelastic part of the stress, τ
v can be
modeled using differential or integral formulations.
Differential models have been traditionally the choice to
simulate polymeric fluids. The general form of a
differential viscoelastic model is given by
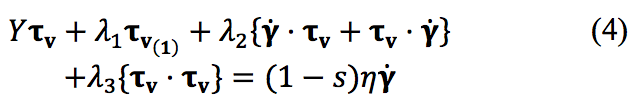
where τ
v(1) is the convected derivative of the deviatoric
stress and it is defined as
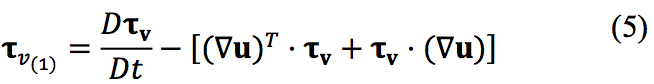
Depending on the definition of the parameters Y, λ
1, λ
2 and λ
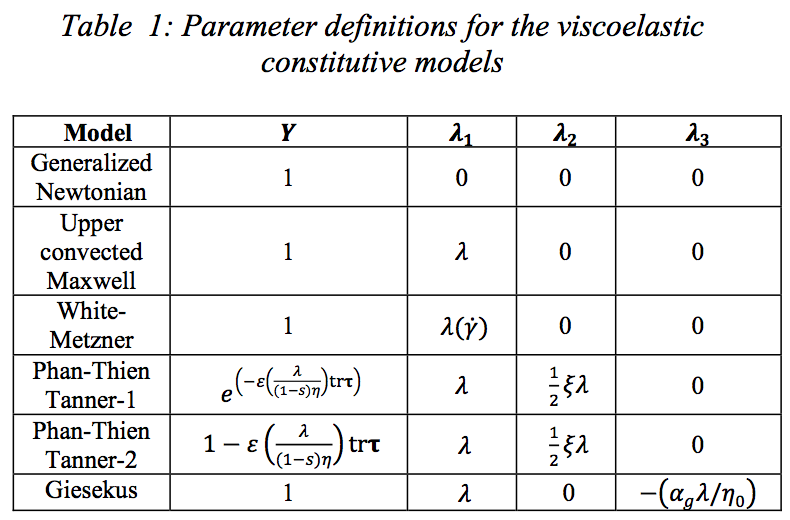
3 the viscoelastic model changes [13]. The
parameter definitions for the most common viscoelastic
constitutive models are listed in Table 1.
The numerical implementation is based on the Radial
Function Method (RFM) which was introduced by Kansa
[6]. This method allows the approximation of a field
variable in a continuous space by a linear combination of
interpolation coefficients and Radial Basis Functions
(RBF). For example, pressure can be written as:
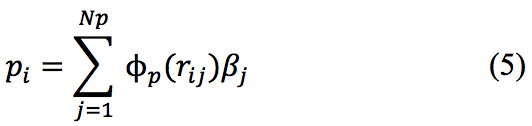
where Beta
j is the interpolation coefficient rij is the distance
between the nodes i and j and theta
p(r
ij) represents the RBF
to interpolate unknown fields. In this work the Thin Plate
Spline (TPS) is used as the RBF.
In a similar way, the velocity components and the
stress tensor components can be rewritten as
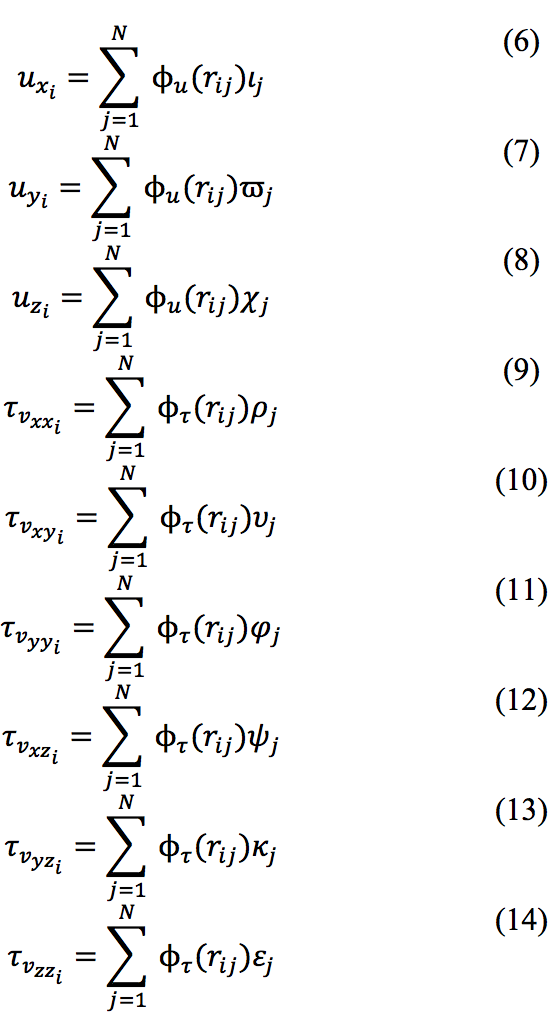
Let us consider a viscoelastic fluid that flows
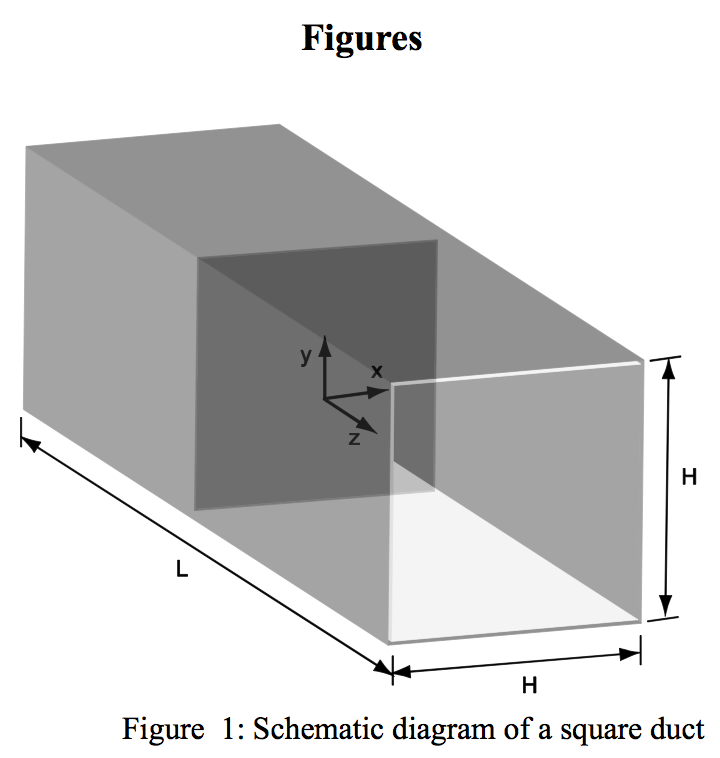
through a straight noncircular duct. Figure 1
schematically depicts the geometry of a square duct. The
main flow direction is defined by the z-axis and the
secondary recirculations occur in the xy plane. The
section is constant along the duct and the flow is assumed
fully developed. Therefore, we can assume that the
pressure drop, ΔP/L and velocity and stress tensor
components are constant in the main flow direction. This
allows the 2-1/2D RFM formulation (a 3D flow where the
velocity field does not change in the z-direction),
requiring only the cross-section of the channel to model
the flow. In that kind of geometry we can assume that the
velocity field does not change in the z-direction. Based on
this assumption, and using τ
N as defined in (3), the x-
component of the momentum equation (2) is simplified as
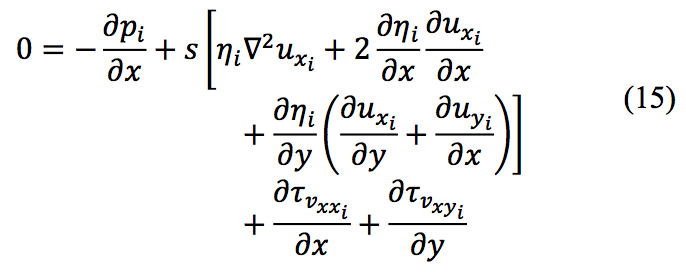
The above equation can be approximated with RBFs
by using the definitions of eqs. (6-14):
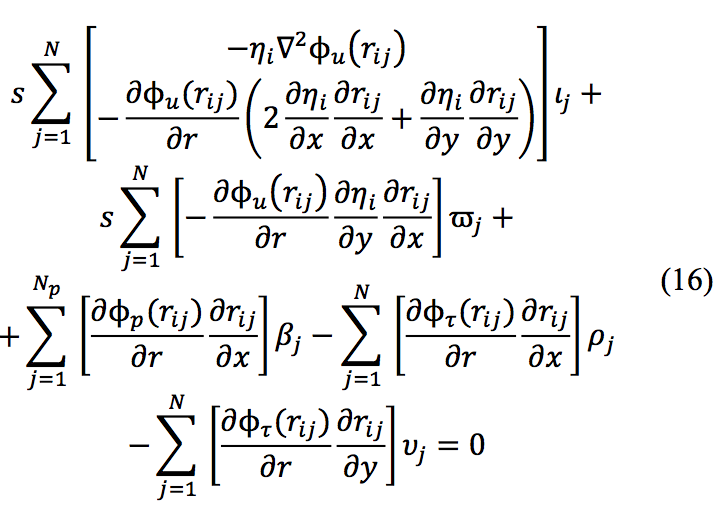
The same procedure should be followed for the other
two components of the momentum equations, the
continuity equation and the constitutive equation
presented in (4). The values for the pressure, velocity and
stress fields can be obtained by applying the boundary
conditions and solving for the interpolation coefficieints.
The stress and rate of deformation tensors of (4) are
unkonwn, requiring an iteration process which starts using
a Newtonian solution.
Results
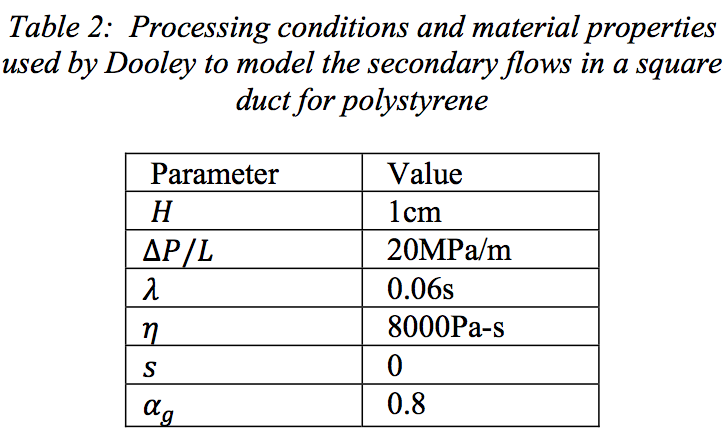
The present work considers the processing
conditions and material properties used by Dooley in his
work [3,4], taking advantage of the possibility of
verifying the results with experimental measurements and
results delivered by other numerical methods.
Square Duct
The first geometry considered is a straight square
duct as the depicted in Figure 1. The material properties
and processing conditions listed in Table 2 are used.
Those conditions are the same used by Dooley in his
experiments and numerical simulations with polystyrene.
The Giesekus equation is considered to model the
viscoelastic effect.
Four hundred nodes uniformly distributed are
considered to approach the solution. When a simulation
was performed using the upper convected Maxwell model
(α
g = 0), no secondary flows were observed. This is
expected since the Maxwell model does not predict the
second normal stress difference which causes the
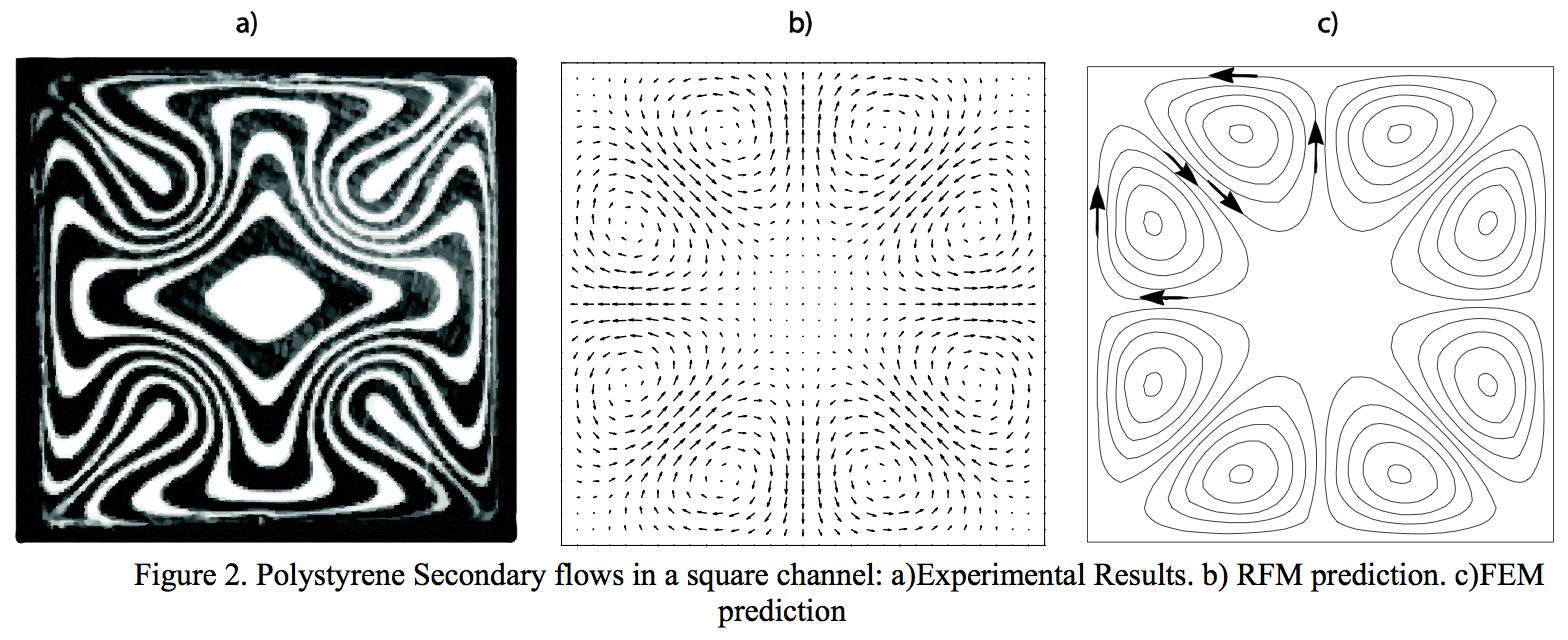
recirculation. Figure 2 compares the secondary flows
delivered by RFM using Giesekus model with the FEM
simulation and the experimental observation of Dooley's
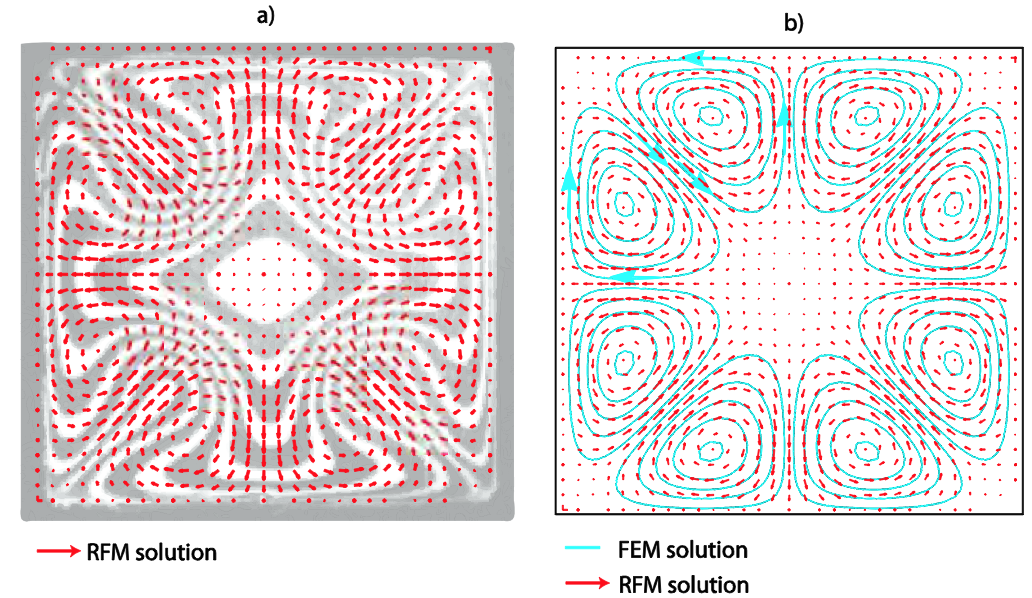
work. The RFM solution is overlapped with Dooley's
observations and simulations in Fig. 3. RFM clearly
predicts the same flow pattern obtained in Dooley's work,
with a good agreement in the estimation of the
recirculation center locations. The secondary flows have
1% the order of magnitude of the main flow, which
coincides with Dooley's FEM results.
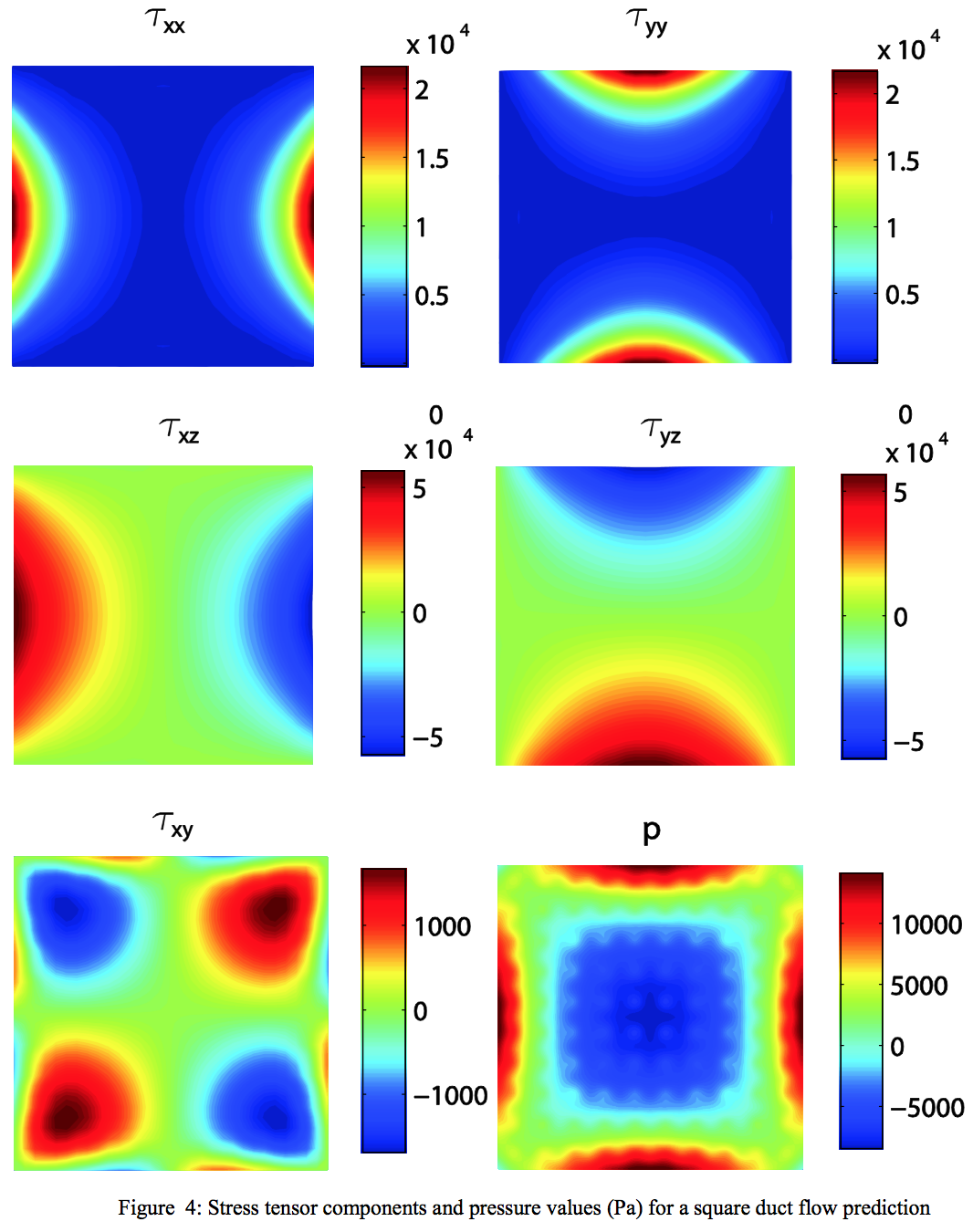
The RFM predictions of the stress tensor components
and pressure variations in the transversal section are
depicted in Fig.4. The theoretical symmetry of the system
is correctly described by RFM. The stress results are
smooth and free of oscillations. Some oscillations can be
appreciated in the pressure solution; however, they do not
seem to compromise the accuracy and smoothness of
velocity and stress tensor estimations.
Teardrop Duct
A teardrop shape duct approximates the geometry
used in many extrusion die distribution systems. The
generation of secondary flows in distribution manifolds
may have important effects in the coextrusion of
multilayer films as discussed by Dooley [3].
The same material properties and processing
conditions used for the square duct were considered
(Table 2). The geometry and dimensions of the teardrop
were defined in such as way that the volumetric flow rate
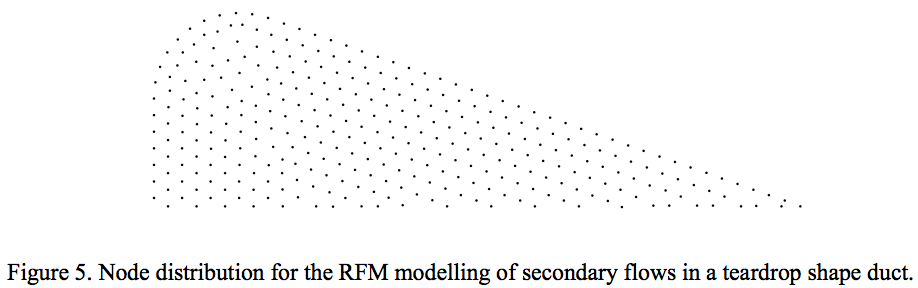
was equal to that of the square duct case. Figure 5 shows
the node distribution used for the simulation. Only a half
of the geometry was considered taking advantage of the symmetry. Three hundred collocation nodes were used
for the solution.
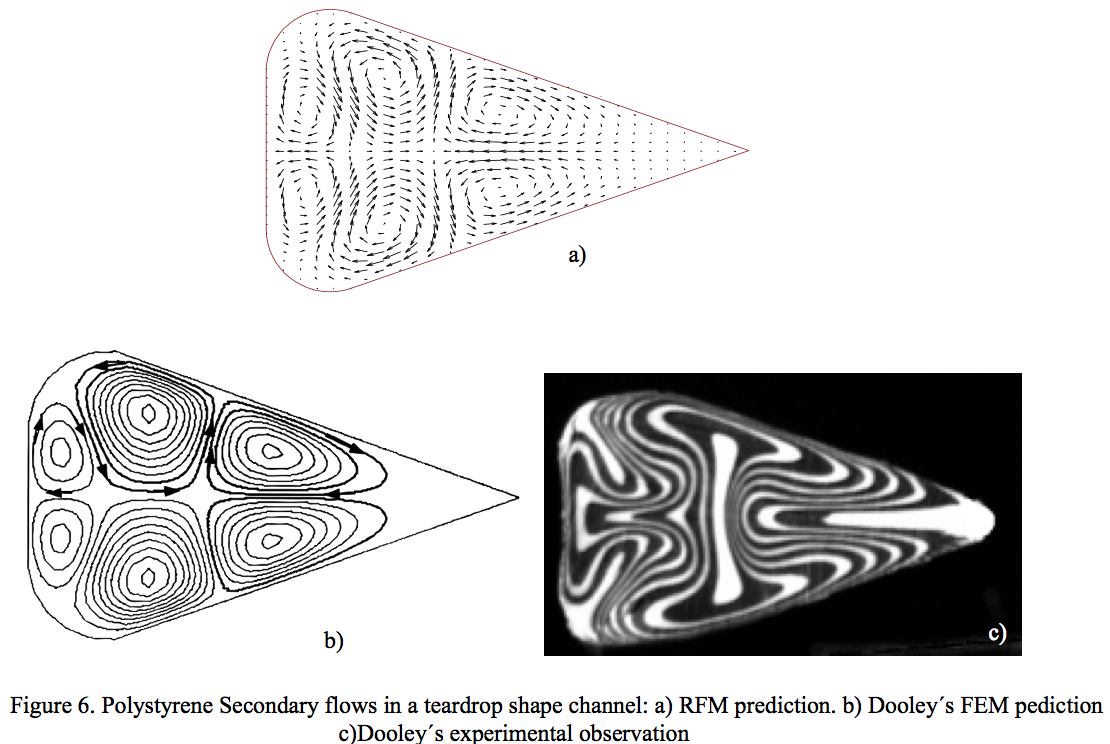
Figure 6 compares the secondary flows delivered by
RFM with the FEM simulation and the experimental
observation of Dooley's work. The numerical solutions
render the same secondary flow patterns observed
experimentally, predicting six vortices where the
strongest secondary flow is along the longest duct
direction.
Conclusions
RFM offers a novel, simplified approach to model
viscoelasticiy. RFM has the potential to solve for
geometries with a high degree of complexity. The cost
benefit of RFM is to use as few nodes as possible while
continuing to increase We.
Nonlinear viscoelasticity was modeled using RFM.
A general formulation that includes Giesekus, Phan Thien
Tanner and Upper Convective Maxwell models was
implemented for two-dimensional flows and flows that
consider the three components of velocity but neglecting
changes in the z-direction. RFM was able to reproduce
accurately the secondary flows in straight noncircular
ducts experimentally observed and numerically predicted
in Dooley's work [3,4].
Future Work
The solution for viscoelastic fluids using RFM
should be extended to higher Weissenberg number (We)
values in order to reproduce actual extrusion conditions.
This can be achieved using relaxation strategies during
the iteration process.
A natural step is to proceed with the simulation of
fully three-dimensional viscoelastic flows, and use the
implementation described in this paper, to study the
elastic effect in extrusion dies.
References
[1] F. Bernal and M. Kindelan. “RBF meshless modeling of non-Newtonian Hele-Shaw Flow”. Engineering Analysis with Boundary Elements, 31: 863 -874, 2007.
[2] B. Debbaut and J Dooley. Secondary motions in straight and tapered channels: Experiments and threedimensional finite element simulation with a multimode differential viscoelastic model. Journal of Rheology, 43(6):1525-1545, 1999.
[3] J. Dooley. Viscoelastic flow effect in multilayer
polymer coextrusion. PhD thesis, Tecnhische Universiteit
Eindhoven, 2002.
[4] J. Dooley and L Schkopau. Viscous and Elastic
Effects in Polymer Coextrusion. Journal of Plastic Film
and Sheeting, 19(2):111-122, 2003.
[5] M. Er-Riani, A. Naji, A. Nouar, and O. SeroGuillaume.
Multiquadrics method for Couette flow of a
yield-stress fluid under imposed torques. International
Workshop on MeshFree Methods Proceedings, 2003.
[6] H. Giesekus. Sekundrstrmungen in viskoelastischen
flssigkeiten bei stationrer und periodischer bewegung.
Rheol. Acta 4, page 85101, 1965
[7] E. J. Kansa. “Multiquadrics - a scattered data
approximation scheme with applications to computational
fluid-dynamics .1.” Computers & Mathematics with
Applications, 19(8-9):127- 145, 1990.
[8] I. D. López, O. Estrada, and T. Osswald. “Modeling
and simulation of polymer processing using the radial
functions method”. Ak Zeitschrift Kunststofftechnik, 2007.
[9] I. D. López, O. Estrada, Noriega M. D. P., and W. F
Flórez. “Collocation method solution with radial basis
functions of the 2d energy equation”. ANTEC, Annual
Technical Conference Proceedings, 2005.
[10] I. D. López, S. Hoffman, A. Bednar, and T. Osswald.
“Filling simulation and temperature prediction in hot
runner systems”. ANTEC, Annual Technical Conference
Proceedings, 2008.
[11] I. D. López, F. Klaiber, and T. Osswald. “Analysis of
viscous heating effect in a pressure slit rheometer using
the radial functions method (RFM)”. ANTEC, Annual
Technical Conference Proceedings, 2006.
[12] N. Mai-Duy and R. I. Tarmer. “Computing nonNewtonian
fluid flow with radial basis function
networks”. International Journal for Numerical Methods
in Fluids, 48: 1309- 1336, 2005.
[13] T. Osswald, López I.D. Hernandez, J.P, and O.
Estrada. Polymer Processing Modeling and Simulation,
Chapter 11: “Radial Function Method”. Hanser, 2006.
[14] J.F.T. Pittman and Tucker III C. L. Fundamentals of
Computer Modeling for Polymer Processing. Hanser
Publishers, 1989.
[15] S. Syrjala, Laminar flow of viscoelastic fluids in
rectangular ducts with heat transfer: A finite element
analysis. International Communications in Heat and
Mass Transfer, 25(2):191-204, 1998.
[16] S. Tanoue, T. Naganawa, and Y. Iemoto. Quasithree-dimensional
simulation of viscoelastic flow through
a straight channel with a square cross section. Nihon
Reoroji Gakkaishi, 34(2):105-113, 2006.
[17] P. Yue, J. Dooley, and J.J. Feng. A general criterion
for viscoelastic secondary flow in pipes of noncircular
cross section. Journal of Rheology, 52(1):315-332, 2008.
Key Words: Viscoelasticity, Giesekus model, Radial Function Method (RFM), Non-circular tubes, Secondary flows, Meshless method.
Return to
Paper of the Month.