Improved Approximations in Thermal Properties for Single Screw Extrusion
Eberhard Grünschloss* and María del Pilar Noriega
ICIPC – Plastics and Rubber Institute
Carrera 49 No. 5 Sur-190, Medellin, Colombia, South America
*Schweitzerstrasse 36, D-70619 Stuttgart, Germany Abstract
Actual screw design software is capable to simulate
the performance of a single screw extruder based on
elaborated program codes. The aim of this work is to
present improved approximations in relevant thermal
properties for simulation and design of single extrusion
screws in combination with analytical calculations
appropriate for the industrial practice. The developed
approximation functions for thermal properties, such as,
specific heat capacity, enthalpy, thermal conductivity and
density, were obtained looking for small number of
parameters. A comparison between the improved
approximation functions, existing known functions and
measured data for some common polymer families is
shown.
Background
The thermal properties of polymers affect the single
screw extrusion process from the feeding zone to the
metering and mixing zone. These properties have an effect
on solids conveying, melting rate and melt conveying of
an extruder screw. The melting rate of the polymer
material has an important effect on extrusion melting
efficiency and it is strongly affected by such properties as
specific heat, thermal conductivity and density obtained
from a p-v-T diagram.
Specific heat capacity describes the amount of
energy that it takes to raise the temperature of a polymer.
LDPE requires an average of 2.596 J/(g.K) in the molten
state, while PS requires 1.95 J/(g.K), [1]. Therefore, it
takes almost 33 % more energy to raise the temperature of
1 g of LDPE than 1 g of PS. Additionally, it means that
more power is necessary to process LDPE than PS at the
same extrusion processing conditions like output in kg/h
and melt temperature. It is well known that the specific
heat capacity is the derivative of enthalpy with respect to
temperature.
Thermal conductivity is the ability of the polymer to
conduct heat. In general, the polymers exhibit a low
thermal conductivity. LDPE has an average thermal
conductivity of 0.25 W/(m.K) in the molten state, while PS is 0.14 W/(m.K), [1]. Because LDPE has a higher
thermal conductivity than PS, the heat flux for LDPE
from barrel to polymer is higher.
Solid and melt density can be obtained from p-v-T
diagram, for example, Tait´s equation of state. The density
is found from reciprocal of specific volume. Nevertheless,
other authors have shown in the literature that Tait´s
equation does not work well for semicrystalline polymers
[2]. The research work of Sanchez-Cho on equation of
state for polymers seems to be until now the most accurate
equation of state [2, 3].
Improved Approximations:
The developed approximation functions for thermal
properties were obtained looking for small number of
parameters, and they are: specific heat capacity for solid
state and molten state, enthalpy for solid state and molten
state, thermal conductivity from the solid state to the
molten state and density from the solid state to the molten
state.
The solid state enthalpy (H
s) is proposed as a fourparameter
function as follows:

Where,
A: Parameter in J/g
B: Parameter in K
C Parameter in K
D: Parameter in K
T: Temperature in K
The enthalpy for molten state (H
m) is proposed as a
two-parameter function as follows:

Where,
F: Parameter in J/(g.K)
E: Parameter in J/(g.K
2)
T: Temperature in K
The specific heat capacity for solid state (Cp
s) is
suggested as a four-parameter function:
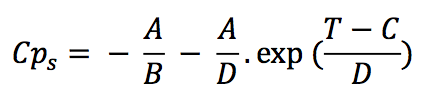
Where the parameters A, B, C and D are taken from the
enthalpy function,
A: Parameter in J/g
B: Parameter in K
C: Parameter in K
D: Parameter in K
T: Temperature in K
The specific heat capacity for molten state (Cp
m) is
suggested as a two-parameter function:
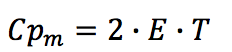
Where the parameter E is taken from the enthalpy
function,
E: Parameter in J/(g.K)
T: Temperature in K
The heat of fusion for semicrystalline polymers can
be obtained graphically from the enthalpy function as
shown in Fig. 1 for a HDPE. The heat of fusion is the
amount of heat energy that is required to convert a
polymer from a solid to a liquid or melt.
The thermal conductivity (k) from the solid state to
the molten state is proposed as one function with six
parameters:
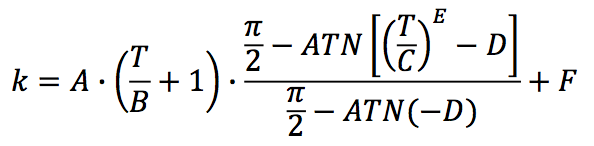
Where,
A: Parameter in W/(m.K)
B: Parameter in K
C: Parameter in K
D: Dimensionless parameter
E: Dimensionless parameter
F: Parameter in W/(m.K)
T: Temperature in K
This function is suitable for the range from room
temperature up to typical melt temperatures in the single
screw extrusion process.
The solid state density (ρ
s) is obtained from
reciprocal of specific volume (υ
s) and it is proposed as a
six-parameter model, as follows:
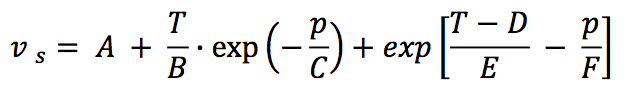
Where,
A: Parameter in cm
3/g
B: Parameter in K
C: Parameter in bar
D: Parameter in K
E: Parameter in K
F: Parameter in bar
T: Temperature in K
p: Pressure in bar
The density for molten state (ρ
m) is obtained from
reciprocal of specific volume (υ
m) and it is proposed as a
three-parameter model after Spencer and Gilmore, as
follows [4]:
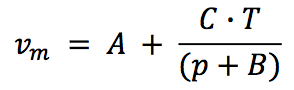
Where,
A: Parameter in cm
3/g
B: Parameter in bar
C: Parameter in (bar.cm3) / (g.K)
T: Temperature in K
p: Pressure in bar
The thermal diffusivity (α) can be calculated from
previous functions, such as, specific heat, thermal
conductivity and density.
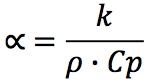
Other Authors have investigated extensions of some
of the above mentioned equations or functions, [5, 6, 7].
The functions described in this work have been found
more suitable for simulation and design of screws in
single screw extrusion, and they were obtained looking for
small number of parameters, what it is appropriate for the
industrial practice.
There is no fundamental theory behind the equations
presented in this paper. This is reasonable because in
practice the polymers are normally not pure but mixed
with additives and reinforcing agents, blended with other
polymers to combine their properties, etc. This will alter
the polymer physics and complicate an appropriate
fundamental theory.
The previous approximation functions contribute to
an easier single screw calculation to simulate the performance of a single screw extruder with regard to
output, pressure build-up, melting rate, heat transfer and
melt temperature. These thermal functions can be used for
the calculations in the screw melting zone, screw metering
zone and extrusion die, Fig. 2, specially, for the prediction
of pressure build-up and melt temperature profile.
Experimental
Polypropylene: a polypropylene homopolymer
reference 505P produced by SABIC with a Melt Index
Flow, MFI, of 2.0 g/10 min at 230ºC/2.16 kg according to
ISO 1133. This is a multipurpose grade for extrusion and
injection molding applications.
Modulated DSC: A Q200 Differential Scanning
Calorimeter from TA Instruments was used for measuring
total heat flow, enthalpy and heat capacity. Test
conditions were carried out following the standard ASTM
E 1269.
A 10 mg of sample was heated from an initial temperature
up to a final temperature under high purity nitrogen, using
a heating rate of 20°C/min. An isotherm at final
temperature is required during 5 minutes.
Results
The solid state enthalpy (Hs) and for molten state
(Hm) for PP Ref. 505P proposed as two functions in
previous numeral have converged to the following
parameters:
A: -971.49 J/g
B: 350.44 K
C: 475.11 K
D: 15.18 K
E: 0.0034 J/(g.K
2)
F: -303.155 J/g
The Fig. 3 shows the measured data and the obtained
approximation functions. From the figure it is possible to
observe that the approximation functions match the data
very well.
The specific heat capacity for solid state (Cp
s) and
for molten state (Cp
m) for PP Ref. 505P proposed as two
functions in previous numeral have the same parameter
values for A, B, C, D and E than the enthalpy functions,
since specific heat capacity is the derivative of enthalpy
with respect to temperature.
The Fig. 4 shows the obtained approximation functions
from measured enthalpy data. This figure illustrates that
the approximation functions match the data properly.
The thermal conductivity (k) from the solid state to
the molten state for a HDPE reported by VDMA [8] has
met the following parameters:
A: 0.19886 W/(m.K)
B: -0.00538 1/K
C: 0.00873 1/K
D: -4.76
E: 16.81785
F: 0.25451 W/(m.K)
The Fig. 5 shows the measured data and the obtained
approximation function. From the figure it is possible to
observe that the approximation function fits the data
satisfactorily.
The solid state density (ρ
s) for a PP measured by
Borealis is obtained from reciprocal of specific volume
and it has converged to the following parameters:
A: 1.042 cm
3/g
B: 3540 K
C: 2166 bar
D: 422.1 K
E: 8.364 K
F: 353.3 bar
The density for molten state (ρ
m) for a PP measured
by Borealis is obtained from reciprocal of specific volume
and it has met the following parameters:
A: 0.9537 cm
3/g
B: 2435 bar
C: 1.8542 (bar.cm3)/(g.K)
The Fig. 6 shows the measured data and the obtained
approximation functions for the solid and the molten state.
From the figure it is clear that the approximation functions
fit the data very well.
The Fig. 7 is demonstrating the use of the above
described thermal functions in combination with
analytical calculations, [9], for the prediction of pressure
build-up in a single screw of D = 20 mm and L/D = 20 for
PE processing. The left ordinate axis shows the screw
pitch, the right ordinate axis shows the screw channel
depth and the abscissa or X-axis is the axial screw length.
Solids bed profiles (SBP) could be obtained for
several polymers and single screws using the experimental
values of X/W versus L/D from a patented device
compared to analytical melting models using the
mentioned thermal functions, [10].
Conclusions
This work presented improved approximations with
reduced number of parameters in thermal properties that
are relevant for simulation and design of single extrusion
screws. These approximations in combination with
analytical calculations are appropriate for the industrial
practice, since they deliver accurate enough predictions of
output and pressure build-up of extruder screws, among
others.
There is no fundamental theory behind the equations
shown in this paper. This is reasonable because in practice
the polymers are normally not pure but mixed with
additives and reinforcing agents, blended with other
polymers to combine their properties, etc. This will alter
the polymer physics and complicate an appropriate
fundamental theory.
The developed approximation functions for thermal
properties, such as, specific heat capacity, enthalpy,
thermal conductivity and density, fitted the measured data
very well. The authors gave an adequate mathematical
representation of the measured data, suitable for inclusion
in future analytical models and papers.
References
/1/ Kühnle, H. and Grünschloss, E., “Berechnung der
Austragszone von Einschneckenextrudern”,
Rheologie in der Kunststofftechnik, Technische
Akademie Esslingen, Ostfildern, Germany, 1999
/2/ Zoller Paul, “PVT Reltionship and Equations of State
of Polymers,
/3/ Cho, J. and Sanchez, I., “PVT Relationship and
Equations of State of Polymers”
/4/ Spencer, R.S. and Gilmore, G.D., “Equation of state
for high polymers”, Journal of Applied Physics, 21,
pp. 523-526, (1950).
/5/ Sanchez, I. and Cho, J., “A universal equation state
for polymer liquids”, Polymer, Vol. 36, No. 15, pp.
2929 – 2939, 2005
/6/ Naranjo, Alberto, “Measurement of the Thermal
Diffusivity of Thermoplastics under Processing
Conditions”, IKV-Berichte aus der
Kunststoffverarbeitung, Mainz, G., Germany, 2004
/7/ Sedlacek, T., et.al. “On relationship between PVT
and rheological measurements of polymer melts”,
Annual transactions of the Nordic Rheology Society,
Vol. 13, 2005.
/8/ VDMA, “Thermodynamik”, Carl Hanser Verlag,
Munich, Germany, 1979
/9/ Grünschloss, E., “Polymer Single Screw Extrusion:
Modeling“, Encyclopedia of Materials: Science and
Technology, Elsevier Science Ltd., 2001
/10/ Noriega, María del Pilar, et. al., “Method and device
to visualize in-line and quantify the polymer melting
in plasticating screw machines without significantly
affecting its thermal regime”, U.S Patent No.
7314363, January 1, 2008.
Acknowledgments
Thanks are also due to the Instituto de Capacitación e
Investigación del Plástico y del Caucho (ICIPC) in
Medellín, Colombia, Institute for Plastics Technology
(IKT) in Stuttgart, Germany, German Academic
Exchange Service (DAAD) and ICETEX in Colombia for
their valuable support to develop this research project.
Nomenclature
D Extruder diameter
L/D Dimensionless Extruder length
X/W Dimensionless screw channel width
H
s: Solid state enthalpy
Hm: Enthalpy of the melt
Cp
s: Specific heat capacity of the solids
Cp
m: Specific heat capacity of the melt
k: Thermal conductivity
ρ
s: Solid state density
ρ
m: Density of the melt
υ
s: Specific volume of the solids
υ
m: Specific volume of the melt
α: Thermal diffusivity
R: Gas constant, 8.3144 J/(mol.K)
p: Pressure
T: Temperature
LDPE: Low density polyethylene
HDPE: High density polyethylene
PP: Polypropylene
PS: Polystyrene
Key Words: Single screw extruder, thermal properties,
specific heat capacity, enthalpy, density, thermal
diffusivity, LDPE, HDPE, PP, PS
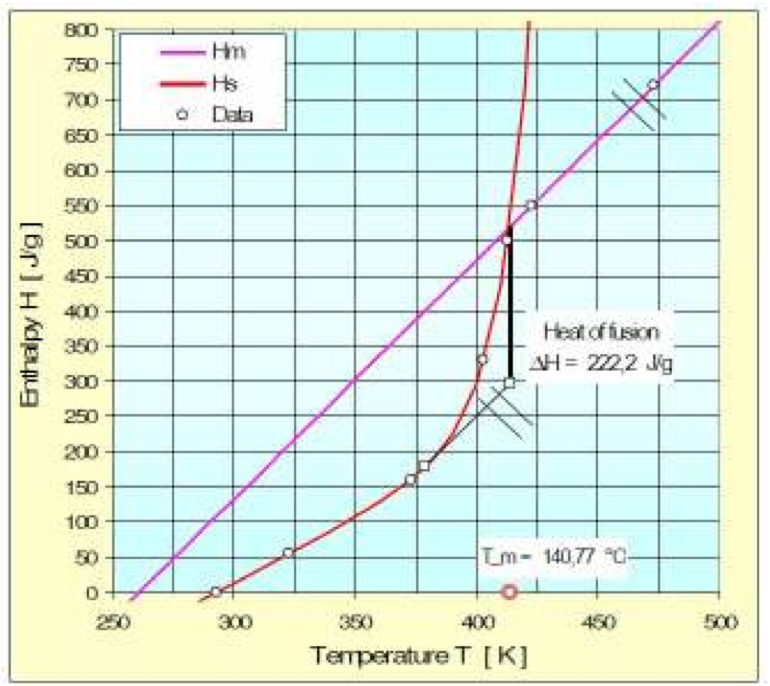
Figure 1: Graphically obtained heat of fusion for HDPE
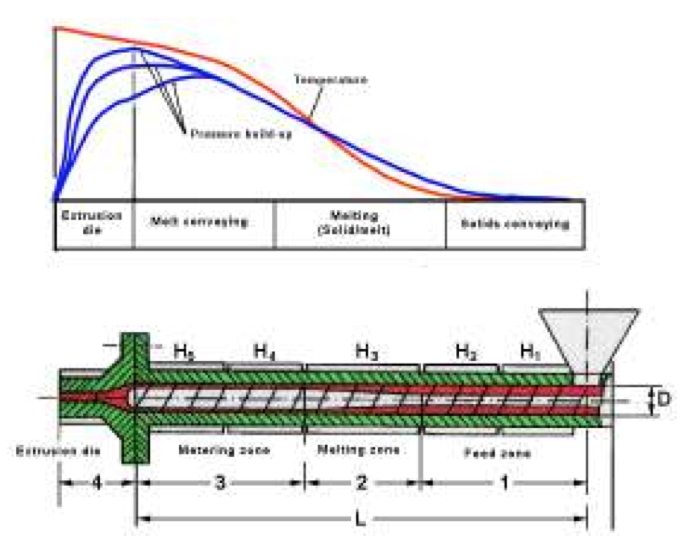
Figure 2: Zones in a single screw extruder
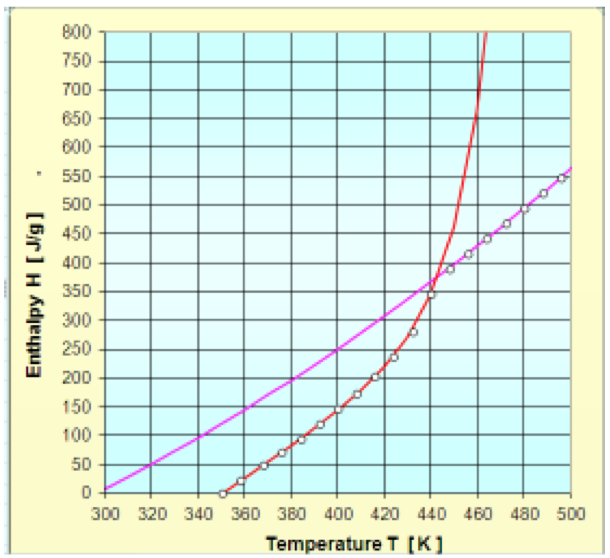
Figure 3: Enthalpy of PP- SABIC 505P: Measured data and approximations

Figure 4: Specific heat capacity of PP- SABIC 505P: Approximations
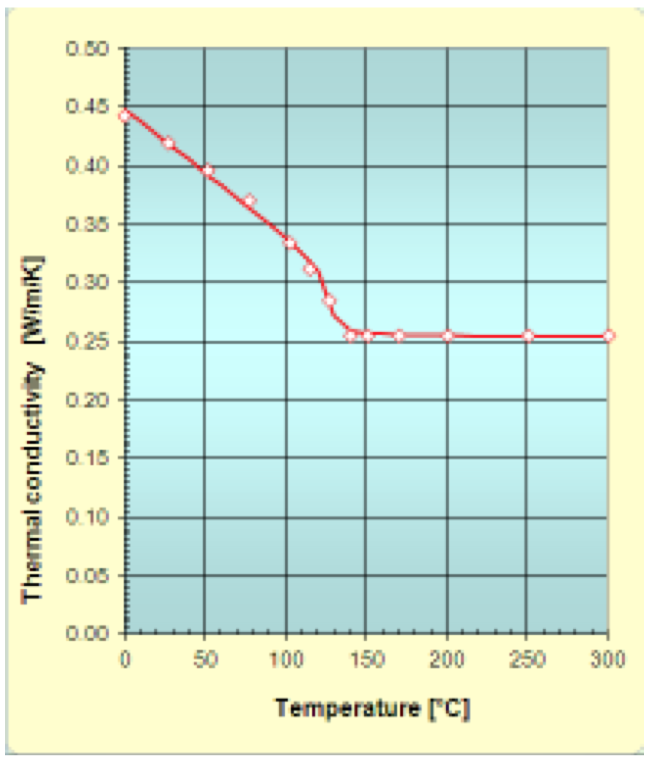
Figure 5: Thermal conductivity of HDPE: Measured data and approximation
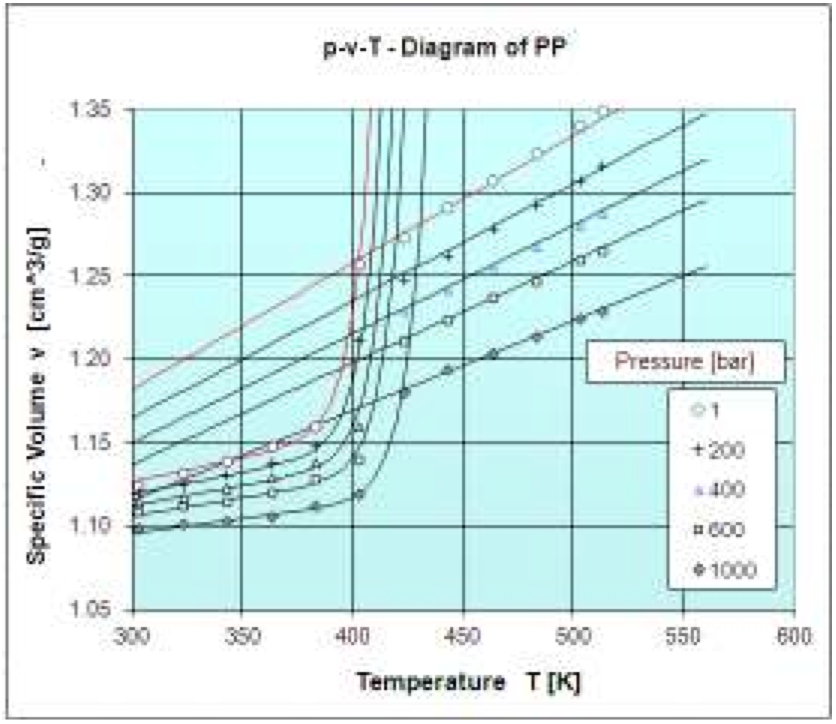
Figure 6: p-v-T diagram of PP (Borealis): Measured data and approximations
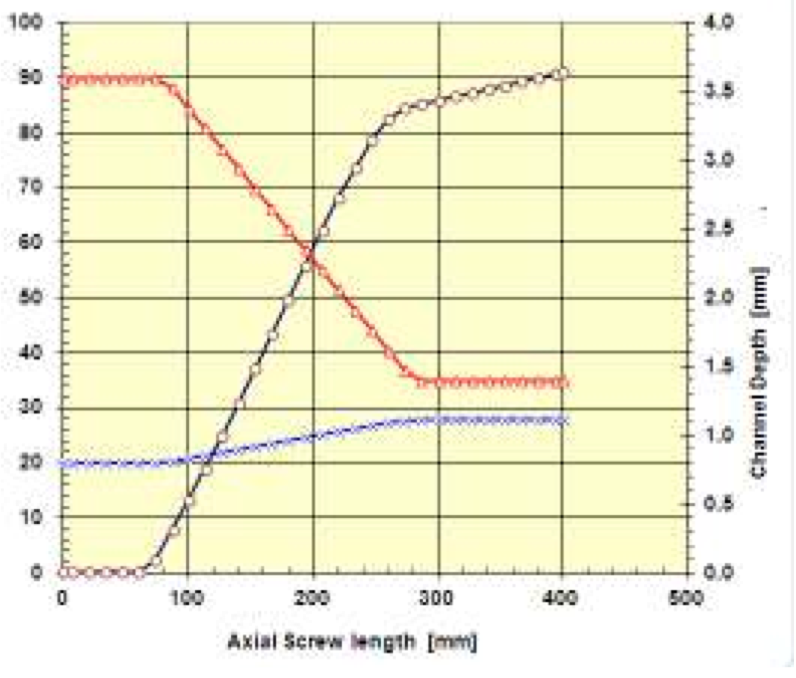
Figure 7: Pressure build-up (ο) of a Ø20 mm screw for PE, channel depth (∆) and screw pitch (x) versus axial screw length
Return to
Paper of the Month.