Distribution of Specific Energy in Twin-Screw Corotating Extruders Using One-Dimensional Process Simulation
Adam Dreiblatt, Century Extrusion, Traverse City, MI
Eduardo Canedo, PolyTech, Campina Grande, BrazilAbstract
Specific mechanical energy (SME) is a single
parameter that represents the energy transfer from the
main drive motor through frictional heating for melting,
mixing and die pressurization in the compounding
process. The calculation of SME is performed using the
extruder motor load (e.g. shaft torque), screw speed and
total throughput to provide energy input on a unit mass
basis. Use of one-dimensional computer simulation to
analyze the axial distribution of specific energy reveals
strategically where this energy is applied in fullyintermeshing,
co-rotating twin-screw extruders as a
function of screw design.
Introduction
Co-rotating intermeshing twin-screw compounding
extruders are the predominant machine in use today for
compounding polymers with additives, fillers, etc. The
compounding process is a complicated sequence of events
whereby polymer(s), impact modifiers and additives are
first melted to create a specific morphology. Particulate
fillers, pigments, etc. are typically introduced into a
downstream feeding port for dispersion into the melt,
followed by a second downstream feeding port for
addition of reinforcing fillers (e.g. glass fiber) or
additional particulate filler with subsequent
homogenization. Finally, volatiles are removed through
vacuum degassing port(s) and the compound is
pressurized through a die or melt filtration device.
For a given formulation, the resulting properties (e.g.
rheological, physical, etc.) are determined largely by the
mechanical energy input to the materials within the
residence time of the compounding extruder. If too much
mechanical energy is applied in homogenizing glass
fibers, for example, the mechanical properties will suffer.
Conversely, insufficient mechanical energy input can also
result in incomplete melting of polymer which will also
produce inferior properties. The interactions between raw
materials (and feeding position), screw design and
operating variables are captured within the single
parameter SME and can therefore be used to correlate
directly with compound quality.
The value of SME is derived from the extruder motor
load (using percent torque instrumentation or direct
measurement of power from the main drive) and represents the cumulative effect of energy input along the
entire screw axis.
This is a similar situation with measurement of
residence time. There are many citations correlating
mixing with residence time distribution (RTD). We can
measure the distribution of residence time using a tracer,
however, this information does not provide insight as to
the distribution of residence time in each element of the
extruder. The only means to obtain such information
would be to measure RTD for each segment of the
extruder. It is physically possible to assemble and operate
an extruder consisting only of the solids conveying
section and measure RTD. Then increase the length of the
extruder by adding a melting section and repeat the RTD
measurements. While a tedious and time-consuming
exercise, the information could be obtained using this
technique.
Similarly, the distribution of specific energy can
provide valuable insight as to where the energy is applied
within the compounding process. As mentioned above, it
would be possible (although time-consuming) to
physically measure the energy contribution of each part of
the screw design by assembling extruders with
incremental lengths.
An alternative to this method uses one-dimensional
(1D) simulation to analyze the mechanical energy
contribution for each part of the screw design. Such 1D
computer modeling programs have been commercially
available and have been validated to provide close
approximations to the actual compounding process
2,3,4.
Simulation provides the capability to measure differential
values along the screw axis for power, temperature,
residence time, etc. and is the basis for this investigation.
The overall energy balance in the processing chamber of
the extruder may be approximately formulated as:
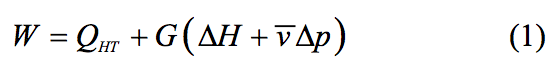
where W is the power delivered to the material, QHT is the
rate of heat transfer between the polymer and the
processing chamber wall (usually the barrel internal wall,
as the screws are assumed adiabatic), ΔH and Δp are
specific enthalpy and pressure difference between output and input, G is mass throughput and v is the mean
specific volume.
For simple systems, ΔH can be easily estimated from the
thermodynamic properties (heat capacities of solid and
molten polymers and fillers, effective latent heat of fusion
of polymers, etc.) in terms of the feed and discharge
temperature and Δp is associated to the head pressure. The
power delivered by the motor may be computed from
measured motor torque and screw speed. Thus, Eq. (1)
may be used to estimate the heat transferred between the
extruder and the material.
Simulation by general purpose software using simplified
one-dimensional models allows the computation of the
power dissipated during compaction and melting of
polymer solids (by friction between the particulate solids
and the barrel wall and screw and between solid particles
themselves, by plastic deformation of the softened solid
particles, etc.) and during the transport and mixing and
pressurization of the molten material (essentially by
viscous dissipation). The heat transport between the
processing chamber and the barrel wall for a given barrel
temperature profile may also be computed (albeit with
greater uncertainty). All these calculations are performed
element by element along the extruder. Likewise,
simulation software computes the internal pressure
profile. Thus, simulation software allows the prediction of
the axial temperature profile, prediction that may be
verified against process data and the models adjusted
accordingly.
Once the simulation software has been validated, the
computation of the power profile along the extruder, or
the mechanical energy input profile (power per unit
throughput), is a powerful tool to investigate where power
is dissipated within the extruder, and how the specific
energy profile depends on screw design and operating
conditions (screw speed, feed rate, barrel temperature
profile, etc.)
With this approach, the individual contribution to
specific energy for each screw element type can be
quantified and optimized for melting and mixing
efficiency as well as for scale-up to larger screw
diameters.
Methodology
The one-dimensional computer simulation program
WinTXS™ from PolyTech was used for this analysis. The
simulations were performed using a polypropylene (PP)
resin with melt index = 5, 10 and 20 dg/min (230
oC, 2.16kg) and a 70 millimeter twin-screw extruder with
diameter ratio = 1.55, length/diameter ratio = 32. The
screw configuration used for simulation is shown in
Figure 1. Die pressure was maintained constant at 30 bar, feed rate was held constant at 1200 kg/hr and screw speed
varied between 400 rpm and 800 rpm.
The energy required to raise the temperature of a unit
mass of a polymeric material from the feed temperature T
1
to the discharge temperature T
2 may be computed,
approximately as:
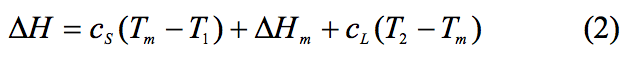
where c
S and c
L are the average specific heats of the solid
and molten polymer, respectively, ΔH
m is the effective
heat of fusion of the polymer (which depends on the
material; for amorphous polymers ΔH
m, = 0), and T
m is
the melting or softening temperature.
The melting temperature for PP was 170
oC and heat capacity 2.34 kJ/kg
oC (solid state) and 1.61 kJ/kg
oC (melt at 200
oC). Shear viscosity data for the MF=5 resin is
shown by Figure 2 using Carreau-Yasuda viscosity model.
Figure 1. Screw configuration used for 70mm simulation
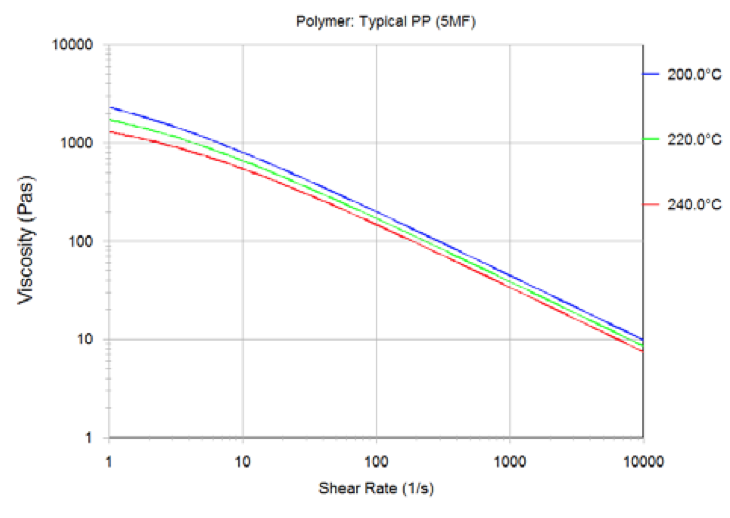
Figure 2. Shear viscosity data for PP resin
Discussion
The net distribution of power along the screw axis is
shown in Figure 3. This curve represents the mechanical
energy input to the extruder and does not account for
energy removed through barrel cooling or the ‘no-load’
power required to turn the motor, gearbox and empty
screws. The contribution of power for each section of the
extruder reveals most of the energy is consumed in resin melting; an energy balance for this section of the extruder
can be used to corroborate the predicted melt
temperatures.
The theoretical energy requirement to raise the solid
polymer from ambient to melting temperature (170
oC) at 1200 kg/hr is 77.75 kW and the theoretical energy
requirement to melt the polymer at 1200 kg/hr is 20.0 kW.
Combining these two, the theoretical energy requirement
for polymer melting is 0.081 kWh/kg. Predicted SME
results for resin melting range from 0.092 kWh/kg at 400
rpm to 0.097 kWh/kg at 800 rpm.
The theoretical energy requirement to raise the
temperature of the melt to predicted discharge
temperature is 40.17 kW (221.5
oC @ 400 rpm), 42.9 kW
(225
oC @ 600 rpm) and 47.6 kW (231
oC @ 800 rpm).
The theoretical SME for the compounding process ranges
from 0.115 at 400 rpm to 0.121 kWh/kg at 800 rpm.
These values are compared to the simulation predictions
in Table 1.
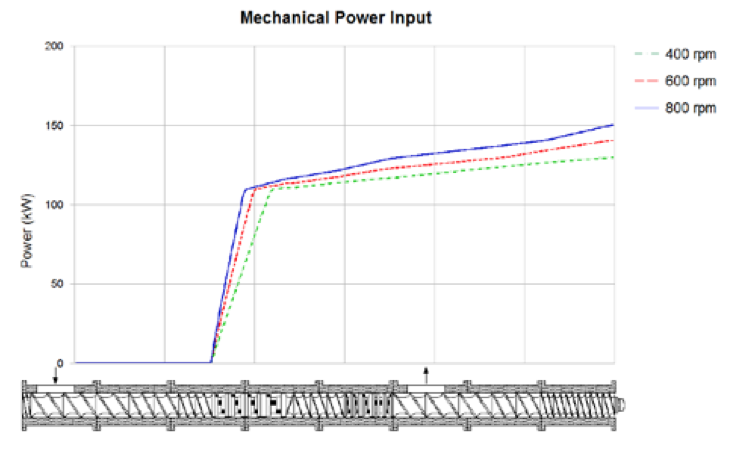
Figure 3. Power consumption versus screw speed
The objective of this investigation is to determine
where this energy is applied along the screw axis.
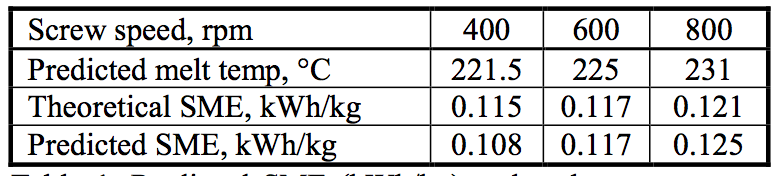
Table 1. Predicted SME (kWh/kg) and melt temperature (°C) versus screw speed.
Solids Conveying
Simulation results indicate zero power consumption
for the initial solids conveying. In reality, given the
available power for a given diameter extruder and the ‘no load’
power to rotate the drive motor, gearbox and screw
shafts, it is not an unreasonable estimate. Typical
industrial extruders do not have the resolution required to measure this small amount of energy. We do not expect
the energy requirement to be more than negligible for
most powders, pellets, flakes, etc. within the range of
most compounds. This situation changes, however, when
melt feeding a twin-screw extruder directly from a reactor
where the power required is for melt conveying (versus
solids conveying).
The process length (in terms of L/D) required for
initial solids conveying is usually in the range of 6D to
8D; increasing the length of the solids conveying section
would not increase the energy requirement. As there is
virtually no mechanical energy expended in this section,
any increase in material temperature is via thermal heat
transfer from barrel heating. Given the low degree-of-fill
of the screws in the solids conveying area and relatively
short residence time (less than 1.5 seconds for the material
to move from the feed barrel to the first kneading
element), the temperature of the solid polymer pellets is
far from its melting temperature.
Polymer Melting
The distribution of mechanical energy within the
melting configuration is a function of screw speed and
feed rate. At high screw speed (i.e. high shear stress), the
plastic deformation of solids occurs within the first
kneading elements. This energy transfer is extended to the
following kneading elements at lower screw speed (i.e.
lower shear stress).

Figure 4. Position of resin melting versus screw speed
Note that the polymer is not yet melted, although
most of the mechanical energy is transferred to the
polymer. This energy is expended to deform and compress
the (solid) polymer resin and results in a rapid temperature
rise as illustrated in Figure 5. Melting (phase change)
occurs in the kneading elements that follow; the specific
kneading elements responsible for melting are determined
by screw speed and feed rate. At high screw speed,
polymer phase change occurs in the third kneading
element while the remaining kneading elements are required to accomplish this same task at lower screw
speed.
Once the polymer is molten, mechanical energy input
deteriorates rapidly in the following kneading elements as
viscous dissipation – this axial change in the rate of
energy transfer is shown as a rapid change in slope (i.e.
flattening) of the power distribution curve in Figure 3. In
this case, polymer melting is completed at the third
kneading element with high screw speed and the
remaining kneading elements are transferring mechanical
energy to the melt increasing the melt temperature. At the
lowest screw speed, there is no mechanical energy input
as viscous dissipation in this first kneading section.
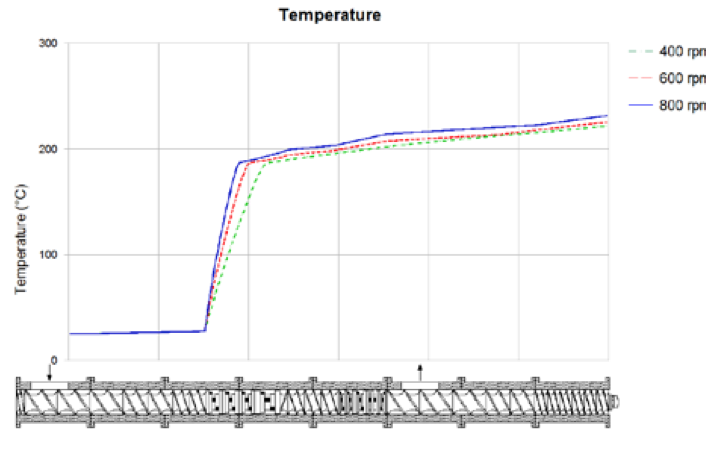
Figure 5. Axial temperature versus screw speed
Most of the energy contribution occurs prior to actual
melting where the temperature increases rapidly (less than
two seconds) as a result of plastic deformation of solids.
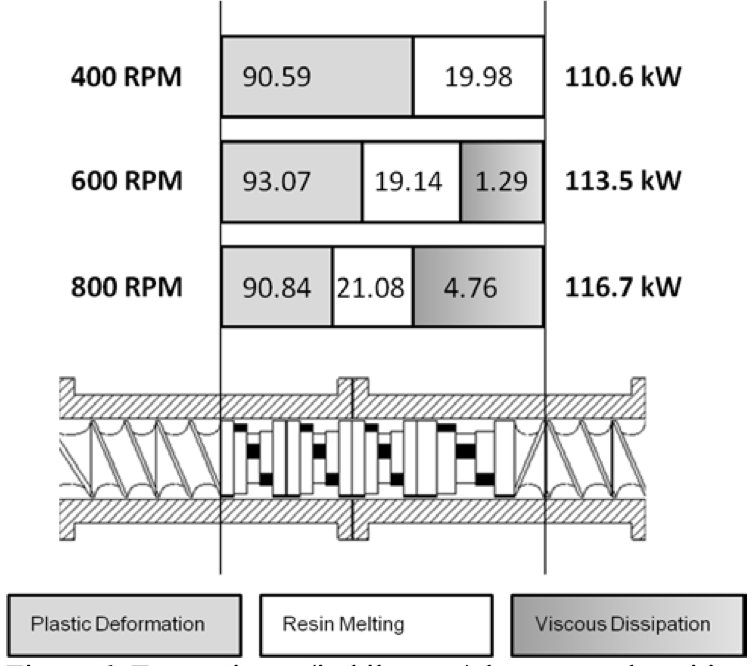
Figure 6. Energy input (in kilowatts) by type and position within the melting section as a function of screw speed
The distribution of mechanical energy within the melting
configuration is shown in Figure 6 where the simulation
predicts the exact position of solids melting as a function
of screw speed. The power distribution curve was used to
quantify the mechanical energy input within the melting
part of the screw configuration by energy type.
Intermediate Melt Conveying
Mechanical energy is applied to the molten polymer
in subsequent conveying sections of the extruder
increasing the melt temperature. Since the polymer
melting represents a substantial percentage of the total
energy requirement, the viscous dissipation of energy in
downstream conveying elements represents only a small
fraction of the total SME and is shown in Table 2. At
increasing values of SME (whether achieved by increased
screw speed, lower throughput or by screw design
changes) the additional mechanical energy is expended in
viscous dissipation since the energy required for polymer
melting is constant.

Table 2. Percentage contribution of SME by function versus screw speed (Melt Flow = 5.0).
The rate of energy input in the downstream melt
conveying section is more depending on the melt viscosity
as shown in Figure 7. In this case, simulations were
performed using PP with different melt flow rates (MF =
5, 10, 20) at the same extruder conditions (1200 kg/hr,
600 rpm) to see the difference in the power distribution in
the downstream melt conveying section.
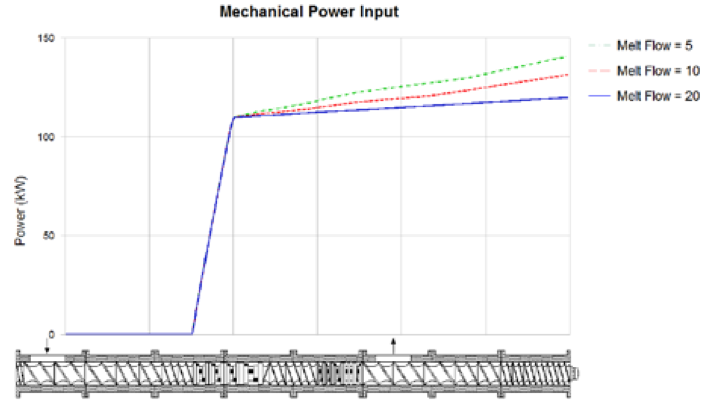
Figure 7. Power consumption (in kilowatts) versus polymer viscosity at 1200 kg/hr and 600 rpm screw speed.
Figure 7 also illustrates the mechanical energy
requirement to melt the PP polymer does not change with
melt flow, however, the resulting viscous dissipation is
strongly affected by polymer viscosity. The flattening of
the power distribution curves (in Figure 7) with decreased
polymer melt viscosity confirms reduced viscous heating.
Melt Mixing
Kneading elements are installed downstream of
polymer melting for dispersive and distributive mixing of
impact modifiers, pigments, additives. fillers, etc. which
may be introduced with the polymer in the main feed
opening or added through downstream feeding. In the case
of downstream feeding, the thermal cooling of the melt
from ambient solids entering the process is not considered
in this investigation (all solids are entering via the main
feed opening, downstream feeding is foreseen in future
work). The mechanical energy input from downstream
kneading elements, as a percentage of total SME, is not
much different than for melt conveying elements as
shown in Table 2.
A second screw design with additional downstream
mixing elements (Figure 8) does not contribute significant
SME as shown in Figure 9. Comparing the slope of the
power distribution curve in this region, there is little
change in viscous dissipation from the additional
kneading elements. The total SME does not change with
this alternate screw design.
Figure 8. Alternate screw design with additional downstream kneading elements.
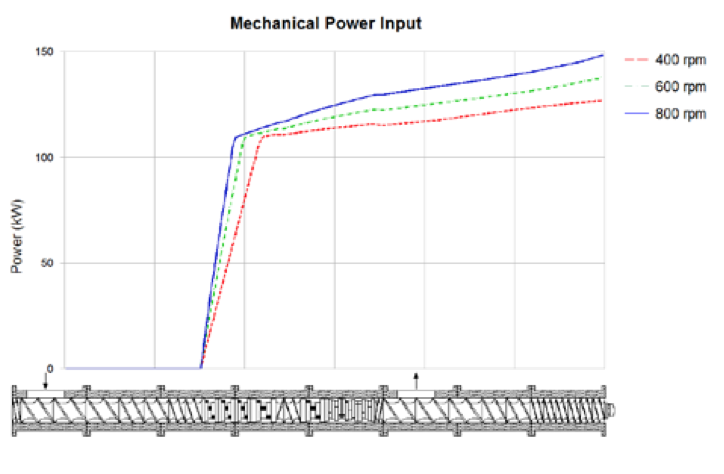
Figure 9. Power consumption (in kilowatts) for alternate screw design with additional downstream kneading elements (PP melt flow = 5, 1200 kg/hr and 600 rpm).
The small increase in viscous energy input in this
downstream mixing section (thereby decreasing melt
viscosity) results in decreased viscous energy input in the
following melt conveying and die pressurization sections.
Die Pressurization
As shown in Table 2, the final melt conveying (e.g. in
vacuum degassing) and die pressurization sections add
between 10 and 15 percent of the total SME. Increasing
conveying length, melt viscosity and SME increases this
percentage. There is little difference, as seen in the slope
of the power distribution curve, in SME input for
conveying with and without pressure (all simulations were
conducted at 30 bar die pressure). The incremental energy
added via viscous heating translates to increased melt
temperature.
Conclusions
One-dimensional computer modeling of the
compounding process provides insight as to where and
how mechanical energy is transformed within the screw
design and enables twin-screw extruder screw designs to
be optimized for melting efficiency and minimizing melt
temperature.
The distribution of specific energy is concentrated in
the first kneading elements where mechanical energy is
applied to the solid polymer prior to actual melting. The
exact position and extent of this energy is dependent on
extruder operating conditions.
SME does not reflect how the energy is applied in
terms of mixing and/or homogenization. What is not
included within SME is the residence time over which the
energy is applied and the resulting shear stress within the
polymer.
Future work will validate some of these predicted
results and investigate SME distribution for downstream
feeding and different screw diameters to confirm scale-up
behavior.
References
1. S. Godavarti, M.V. Karwe, Determination of Specific
Mechanical Energy Distribution on a Twin-Screw
Extruder, J. Agricultural Engineering Research, 67, 4,
277-287 (1997).
2. H.Potente, J. Ansahl, B. Klarholz, Design of Tightly
Intermeshing Co-Rotating Twin Screw Extruders, Intl
Polymer Processing IX, 1, 11-25 (1994).
3. K. Kohlgrüber, Modeling: Possibilities and
Limitations, Co-Rotating Twin-Screw Extruders, Carl
Hanser, 114-117 (2008).
4. E. Canedo, Computer Simulation of Plastics
Compounding Operations in Twin-Screw Extruders,
SPE-ANTEC Tech Papers (1999).
Return to
Paper of the Month.