Lateral Stress and Density Measurements for PC, ABS, HIPS, and PP Bulk Resin Feed Stock¶
Stephen J. Derezinski, Extruder Tech, Inc., Penfield, NY 14526Abstract
A special test device [1-3] was used to make
laboratory measurements of the lateral stress and bulk
density of four resin feed polymers: polycarbonate (PS),
acrylonitrile butadiene styrene (ABS), high impact
polystyrene (HIPS), and polypropylene (PP). The data are
all presented as a function of primary compressive stress
on the bulk pellet resin feed stock. Data for lateral stress,
lateral stress ratio, and density are shown, and regression
functions are provided. Data for the bulk temperature rise
during compression are also provided.
Introduction
Lateral stress has been shown to be a factor in
solids conveying [2] as it is the driving force that creates
the frictional force on the barrel and screw that governs
solids conveying. The same frictional force is also key to
the onset of melting where higher lateral stress gives
higher rubbing friction on the barrel to initiate melting
sooner. More time (or extruder length) for melting results
in more complete melting which is key to stable flow and
pressure.
Materials
PC (DOW Icalibre 300-6), ABS (DOW Magnum
342EZ), HIPS (DOW Styron 1170), and PP (DOW
DX5E66) resin feed stocks in pellet form were analyzed.
Sample sizes of about 4 grams were used, and two samples
were tested for each resin. All temperatures were close to
27
oC. Figure 1 pictures the four resin feed stocks used for
this study.
Experimental Equipment
Figure 2 shows the test cell from previous
work [2,3] used to measure the stresses and bulk density of
the different resins. The instrumentation consists of two
load cells (primary load and lateral load), a linear
displacement transducer (specimen length), and a
thermocouple (resin bulk temperature). The dimensions
of the test chamber and the specimen length provide data
to calculate the bulk density of the sample as a function of
stress. The two load cells and the dimensions of the test
chamber give the needed data to calculate the axial and
lateral stresses developed during compression.
The experimental technique used here establishes
the starting point of compression by connecting the
displacement transducer directly to the top cylinder as shown in Figure 2. The ram of the press (not shown in
Figure 2) is not connected to the top cylinder. Therefore,
the origin of the data of each load cell data is precisely set
when the displacement transducer records compressive
strain as the press ram is lowered.
Temperature of the resin in the sample is
monitored during the test, and this has been added since
the last report [3]. A thermocouple made of 30 gauge wire
was made by twisting the wire pair to approximate the
bulk temperature. The thermocouple extended half of the
distance (~6 mm) across the diameter (~12 mm) of the cell
cavity. The small size of wire minimized the effect of its
presence on the compressive strain and had optimized
response time. The initial value and maximum values of
temperature are recorded. All resins had an initial bulk
temperature of about 27
oC.
Lateral Stress vs. Primary Stress Data
Figures 3-6 show the raw data for lateral stress
versus primary stress for the four polymers, PS, ABS,
HIPS, and PP. The data are repeated to provide two data
sets (1 and 2) for each polymer. As can be seen, the
variation in lateral stress versus primary stress is slight for
PC, HIPS, and PP, but is noticeable for ABS in Figure 4.
This suggests that the variation in lateral stress for ABS
may be unique to it.
Lateral Stress Regression Functions
Regression curves for the data of lateral stress
versus primary stress shown in Figures 3-6 are given in
Figure 7. The data for each of the two sample runs of each
polymer shown in Figures 3-6 are combined and fitted
with the regression function (trend line). A (0,0) intercept
is assumed (zero primary stress = zero lateral stress). The
trend line consistently used is a 6
th order polynomial. Four
trend functions for lateral stress (y) versus primary stress
(x) are given below as follows:


Figure 7 clearly shows the relationship between
the lateral stresses for the four polymers. PP has the
greatest value of lateral stress while PC has the lowest
lateral stress function. ABS and HIPS appear to be very
comparable, which is logical since they are both styrene.
However, it is not generally the case that the same general
polymer has similar lateral stress as was shown for lateral
stress measurement of three polyethylene resins; LLDPE,
LDPE, and HDPE [2].
Equations 1-4 are only applicable within the
shown specified limits of primary stress. Extrapolation
above the upper limit will likely result in large error.
Limited extrapolation above the upper limit of primary
stress should be done with a linear trend line, if need be.
Lateral Stress Ratio Functions
The lateral stress ratio is defined as the ratio of
the lateral stress divided by the primary stress. The lateral
stress ratio function of primary stress is useful in modeling
solids conveying as it provides a convenient mathematical
method for including lateral stress as the product of stress
ratio and primary stress. The lateral stress ratio also
provides more detail about the lateral stress that is not
obvious from the lateral stress versus primary stress data
(Figures 3-6). This is particularly true at low stress levels
(inlet to solids conveying situation), so it is important to
the analysis of every solids conveying process. Figures 8-
11 show the lateral stress ratio functions calculated from
the raw data of lateral stress shown by Figures 3-6.
The resulting equations for stress ratio are the
same as Equations 1-4 but with the exponential power of
each term reduced by a value of one. Equations 1-4 are 6
th
order polynomials, so lateral stress ratio functions are then 5
th order polynomials. Figure 12 plots the resulting 5
th order equations for each of the four resins tested, and comparison to the raw data of Figures 7-10 shows that the 5
th order polynomial approximates the data well. Figure
12 demonstrates more detail about the lateral stress than
does the raw data of lateral stress in Figures 3-6.
The lateral stress ratio as defined cannot be
calculated from the raw data at zero primary stress (0/0 has
no mathematical result). This is obvious from Figures 8-
11 by the sporadic nature of the curves near zero primary
stress. However, the 5
th order function for lateral stress
ratio has a constant term that is the limit for lateral stress at zero primary stress. This limit provides a single value
unique for each resin that indicates lateral stress at the
entrance to solids conveying. Table 1 summarizes the
limit of stress ratio at zero primary stress.
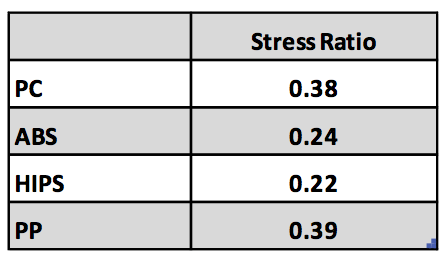
Table 1 Stress Ratio Limit at Zero Primary Stress
Bulk Density
Data: The bulk density of each of the four resins
was obtained from the measurement of compressive strain
and measured mass of the sample. Data for the bulk
density are plotted as a function of primary stress in
Figures 13-16. The data show the full cycle of
compression to the maximum value of primary stress and
then the reverse to zero primary stress. Excellent
agreement between each of the two trials of all four
samples is evident from the data of Figures 13-16.
Regression of Density Data: Trend curves were
obtained for the bulk density data of Figures 13-16. The
trend curves are for only the compressive leg of the density
data. Figure 17 shows the regression curves so obtained,
and extrapolation to 30 MPa of primary stress is
illustrated. The regression equations for density (y) versus
primary stress (x) in Figure 16 are given as follows:

Energy Balance
Plastic Deformation: Mechanical energy used
for the compression of the resin sample by the test cell is
calculated by integration of the density versus primary
stress data shown in Figures 13-16 according to a method
previously given [1]. Integration for compression to
maximum stress provides the total energy. Integration
during the reverse of the load to zero provides elastic
energy of the specimen. The plastic energy is the total
energy less the elastic energy. The results shown in Table
2 give the ratio of plastic energy to total energy. This is
then used to characterize the ability of the polymer “solid
plug” to elastically expand during melting to maintain
solid contact (high rubbing friction) with the barrel for
efficient melting. The high plasticity (low elasticity)
calculated here is detrimental to maintaining solids contact
with the barrel when the solids plug is being eroded by the
removal of melt. Low plasticity (high elasticity) would
provide better conditions for efficient melting, and
extrusion process data for this effect were previously cited
[1]. Good screw design with proper compression section
length can alleviate this issue.
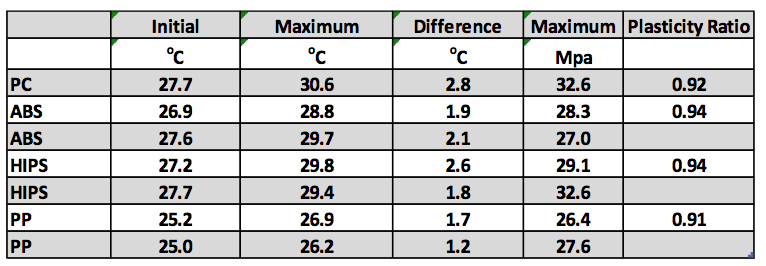
Table 2 Temperatures, Maximum Stress, and Plasticity Ratio
Heat Generation: Temperature measurement of
the polymer during the test was used to investigate the
temperature change that may accompany heat generation
during compression of the resin. A thermocouple was
located (see Figure 2) in the center of the polymer sample
to register the initial and maximum bulk temperature
during the test, and the results are shown in Table 2. The
temperature was found to increase, and the level of
increase was from about 1 to 3
oC for all four resins.
Summary
Lateral stress and bulk density were measured for
four feed resins, PC, ABS, HIPS, and PP. Data for
primary stress up to about 30 MPa show that the lateral
stress of the bulk feed does depend on the polymer. The
stress ratio is used as a function of primary stress to
provide details of the lateral stress and provide an efficient
mathematical method for incorporating lateral stress into
computational models. Regression equations are provided
for such use in computational applications.
The bulk density of the resins was accurately
measured, and regression equations for it are given. The
plasticity of the resin feed is calculated from the
compressive energy based on the density versus primary
stress data and shown to be over 90% for all resins tested.
Finally, the phenomenon of bulk temperature increase
during compression of the resin feed is measured to be up
to 3
oC for the resins tested here.
Conclusions
1. The lateral stress for PP was measured to be the
greatest. The lateral stress ratio was close to 0.4
over the entire primary stress range (0-20 MPa).
2. The lateral stress for the PC was the lowest, and the
lateral stress ratio was about 0.3 over most of its
range. However, it had a lateral stress ratio of up to
about 0.5 at initial primary stress levels. This
relatively high initial stress ratio was unique among
the four resins tested.
3. The lateral stress for ABS and HIPS (both styrene
resin) were measured to be very similar and
between that of PC and PP.
4. The lateral stress ratio for ABS and HIPS was just
above 0.3 over most of the measured range. Low
initial values of about 0.23 greatly differentiate
these resins from PC and PP with initial stress ratios
of about 0.4.
5. Heat is generated during the compression of bulk
resin feed stock as measured by an increase in bulk
temperature of 1 to 3
oC.
6. The energy of plastic deformation for all resins was
above 90% of the total energy of compression as
calculated by integration of the density versus
pressure data.
Acknowledgements
Very special thanks to son, Stephen J. Derezinski,
III of Platform Technology Ventures, Inc., for specifying
the temperature measurement equipment appropriate for
this experimental work.
References
1. S. J. Derezinski 2009. “Laboratory Measurements of
Resin Bulk Specific Gravity of PET and LDPE,”
ANTEC 2009-Proceedings of the 67th Annual
Conference & Exhibition, Chicago, IL, June 22-24,
2009, Society of Plastic Engineers, pp. 136-141.
2. S. J. Derezinski 2010. “Measurements of Biaxial
Stresses During the Compression of Bulk Resin
Feed,” ANTEC 2010-Proceedings of the 68th Annual
Conference & Exhibition, Orlando, Fl, May 16-20,
2010, Society of Plastic Engineers, pp. 617-622.
3. S. J. Derezinski, “Lateral Stress and Bulk Density of
PET Resin with Recycle”, ANTEC 2011-
Proceedings of the 69th Annual Conference and
Exhibition, Boston, Ma, May 1-3, 2011, Society of
Plastic Engineers, pp 100-100.
Key Words
Stress, bulk density, solids conveying, single screw,
extrusion, pellets, biaxial stress, plastic resin, bulk
properties
Figure 1. Four Resins Tested

Figure 2. The Test Cell for Measuring the Primary and Lateral Forces During Compression of Bulk Resin Feed as a function of bulk density [1,2]. Diameter of the cylinder is 12.7 mm. The linear displacement transducer records the height of the sample to establish the evolving bulk density value and lateral area of force. A thermocouple is centered in the resin to obtain the starting and maximum temperatures during compression.
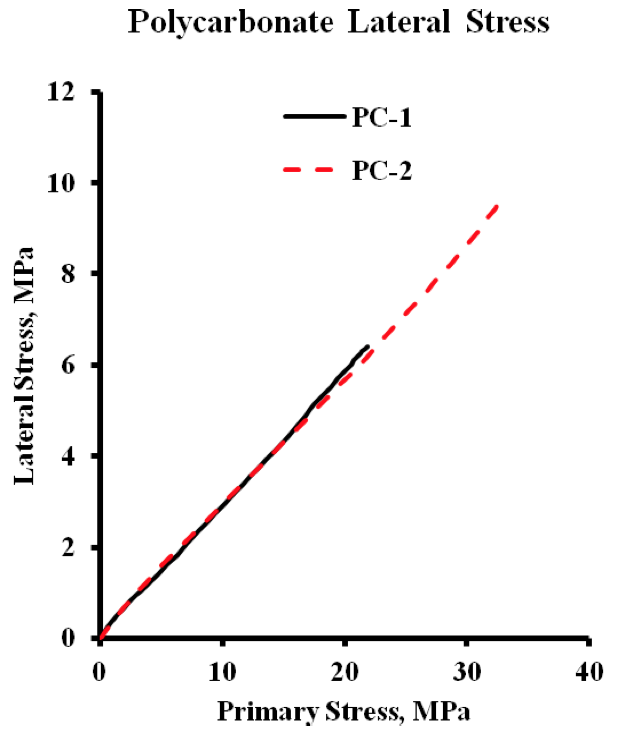
Figure 3. Polycarbonate Lateral Stress versus Primary Stress Raw Data
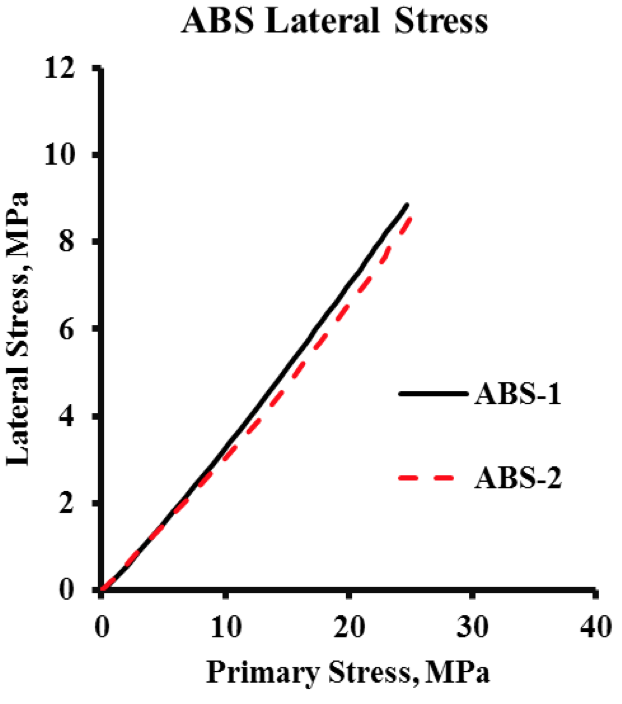
Figure 4 Lateral Stress Raw Data for ABS Resin
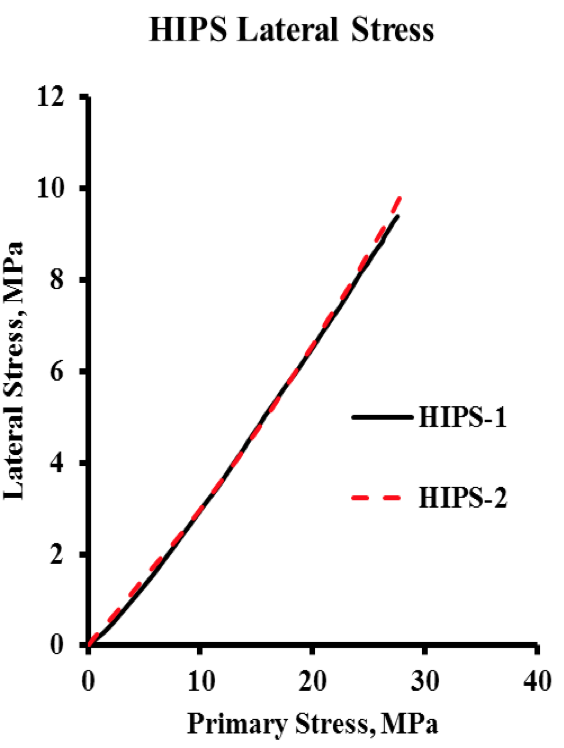
Figure 5. Lateral Stress Raw Data for HIPS

Figure 6. Raw Data for Polypropylene Lateral Stress
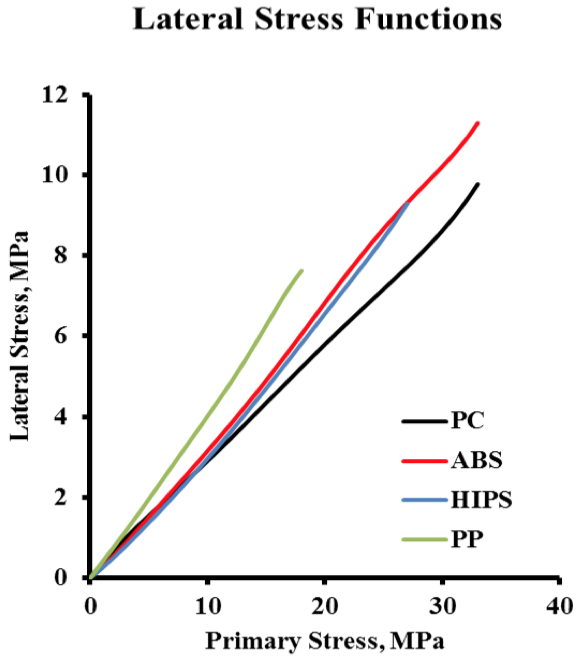
Figure 7. Lateral Stess Function for Four Polymers. Curves obtained by regression analsysis of two data sets
for each of the four polymers (Figures 3-6).
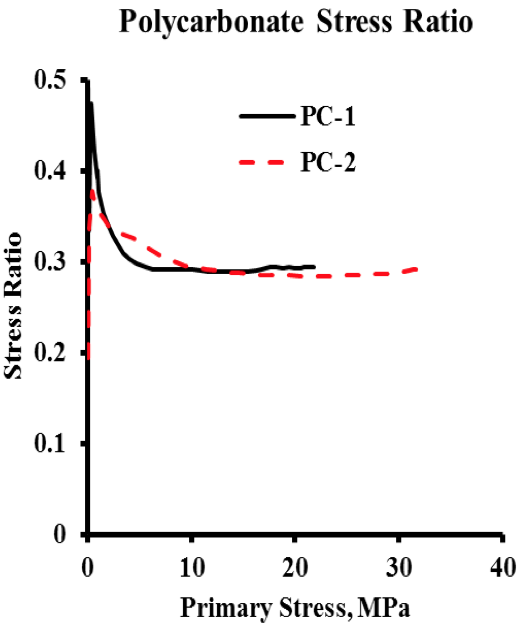
Figure 8. Polycarbonate Stress Ratio Data versus Primary Stress. Curves calculated from data of Figure 3.
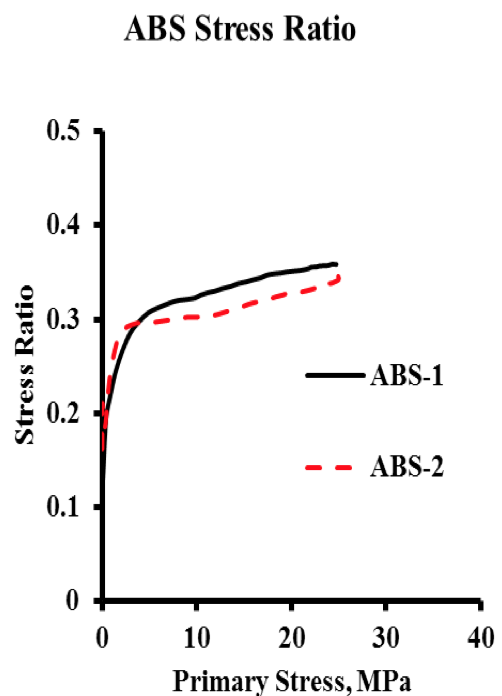
Figure 9. Stress Ratio for ABS Resin. Raw data of Figure 4 used to calculate the stress ratios.
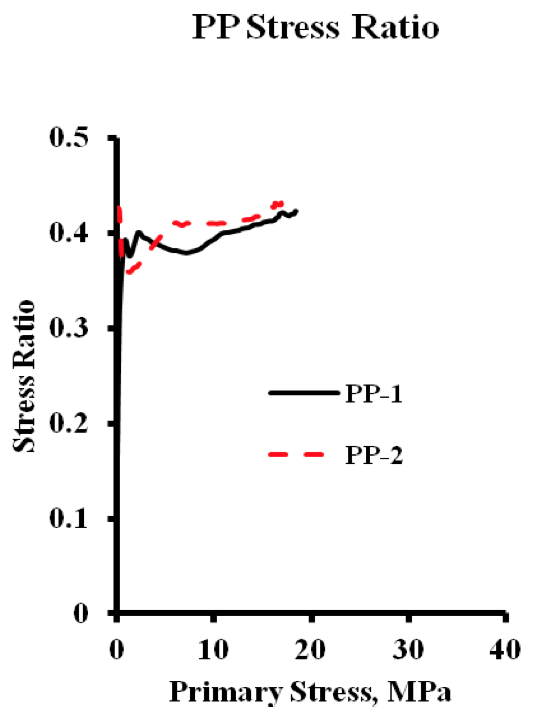
Figure 10. Lateral Stress Ratio for HIPS. Curves calculated directly from raw data of Figure 5.
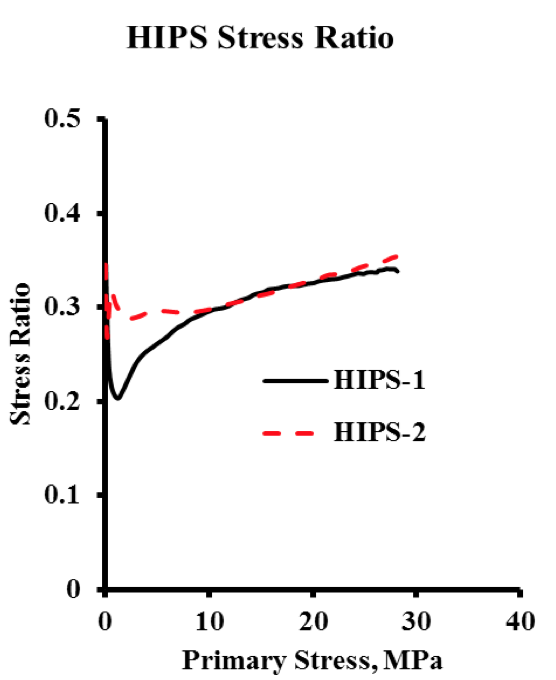
Figure 11. Stress Ratio for Polypropylene Curves calculated directly from raw data of Figure 6.
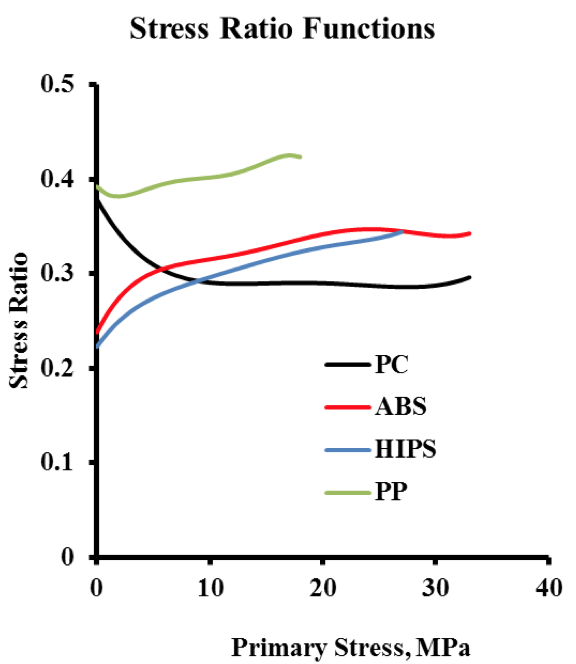
Figure 12. Lateral Stress Ratio Functions for Four Resins The curves are based on the regression equations, Equations 1-4, represented in Figure 7. The lateral stress ratio functions are obtained from Equations 1-4 by merely lowering the exponent in each term by a value of 1.
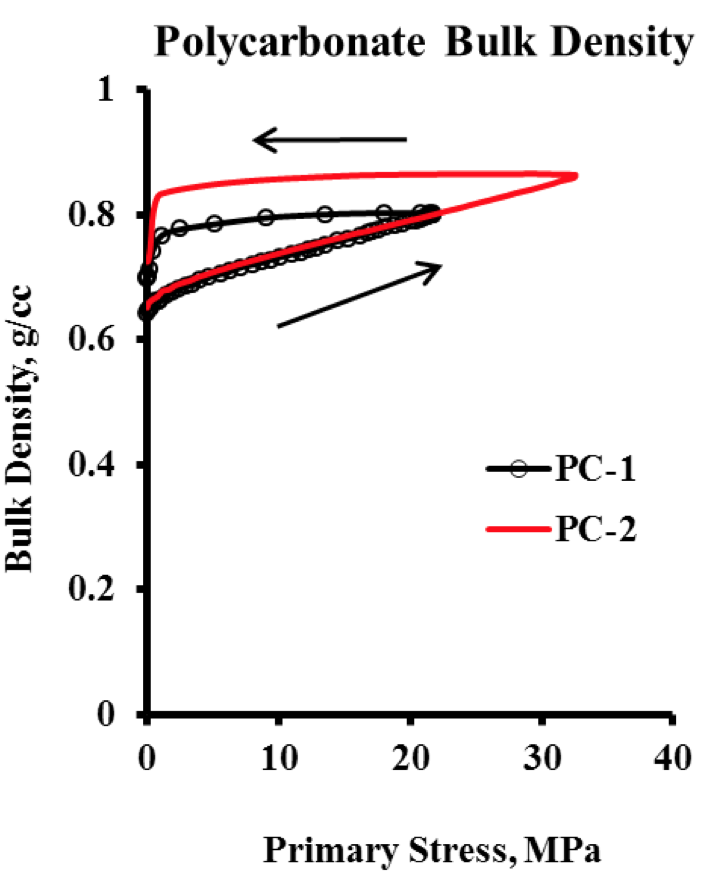
Figure 13. Raw Data for Polycarbonate Density versus Primary Stress. Two samples shown. Arrows indicate compression and release.
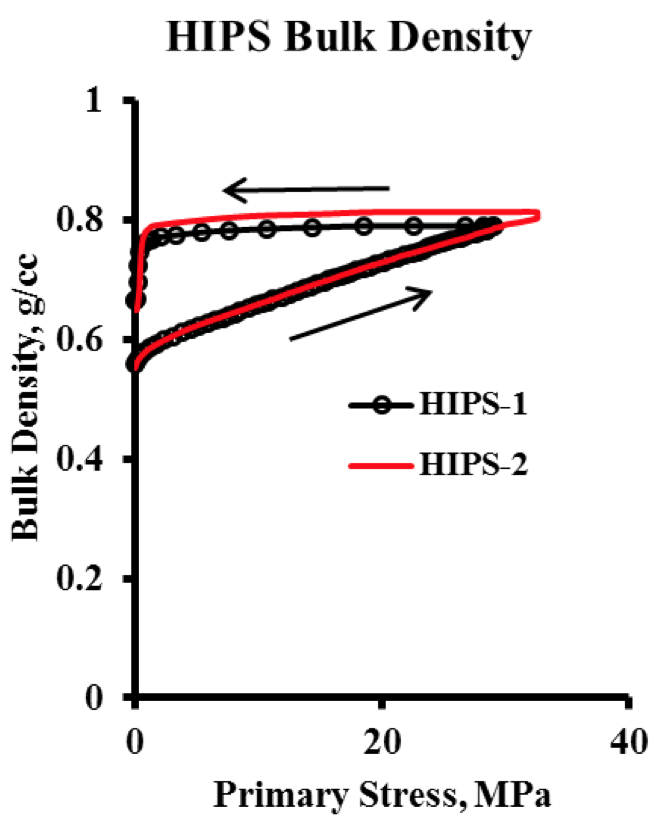
Figure 14. Raw Data for Density of Two ABS Samples. Arrows indicate compression and release.
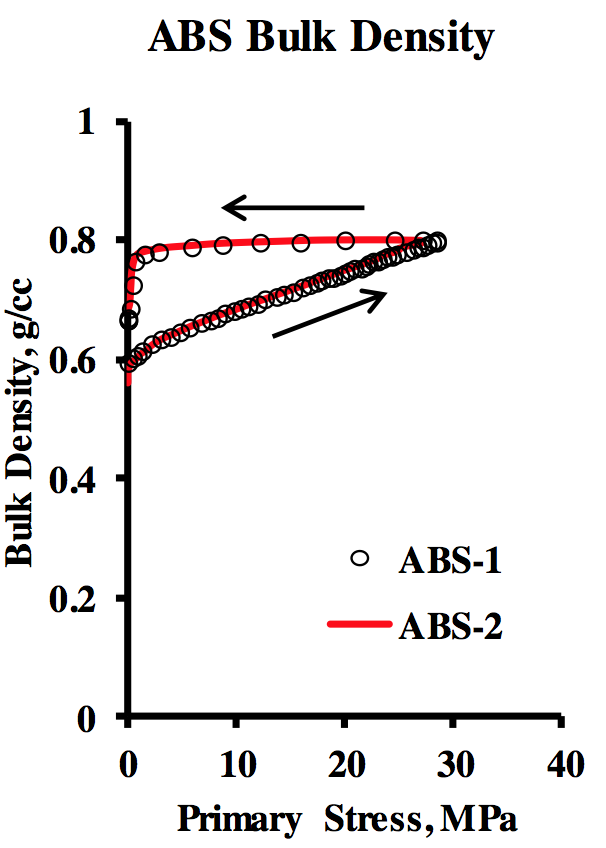
Figure 15, Raw Density Data for HIPS Resin Density Arrows indicate compression and release.

Figure 16. Raw Data for Bulk Density of Polypropylene Arrows indicate compression and release.
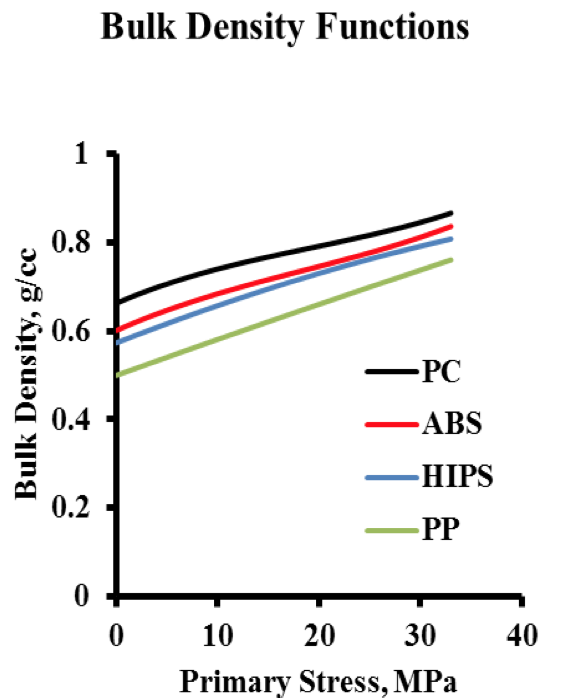
Figure 17. Regression Curves for Bulk Density of Four Resins Only the density during the compression of each resin is shown See Equations 5 to 8.
Return to
Paper of the Month.