"Wave" Pattern Instability in Multilayer Coextrusion: An Experimental Investigation
R. Ramanathan, R. Shanker, T. Rehg, S. Jons, D.L. Headley, and W.J. Schrenk - Dow Plastics, The Dow Chemical Company, Midland MI 48674
Abstract
Flow instabilities are a limiting factor in most multilayer coextrusion processes. Based on topography these instabilities may be classified into three distinct types: 1. zig-zag, 2. scattering, and 3. wave. This report deals with "wave" instability. Recent experimental work has shed light on this least recognized and poorly understood class of multilayer instabilities. It appears to be affected by die design and structure asymmetry. A primary rheological discriminator appears to be the extensional viscosity of the polymers.
Introduction
Multilayer composite sheet structures are well known to offer performance advantages over single component sheet especially when a combination of properties are desired [1]. In many applications multilayer coextrusion offers economic and technical advantages as opposed to coating or laminating techniques.
Multilayer coextrusion is sometimes susceptible to various flow instabilities that compromise the performance or aesthetics of the extruded sheet. At present, three distinct flow instabilities have been identified: zig-zag, scattering, and wave. As their descriptive names indicate, each instability is manifest in the extruded sheet with a distinct pattern. The zig-zag instability appears in the extruded sheet as a series of chevrons pointing in the flow direction. Studies [2,3] have demonstrated that zig-zag is initiated in the die land and is characterized by a critical interfacial shear stress above which the instability occurs. Any means of reducing the interfacial shear stress below the critical value will eliminate the zig-zag instability; i.e. reduce the viscosity, reduce the flow rate, etc. The simplest system where zig-zag has occurred is two layers of the same resin.
Scattering is a disruption in the continuity of a microlayer [4]. It is distinct from zig-zag; scattering is observed only when many layers are present (>100), the individual layers are very thin (<10ìm), and adjacent layers are composed of different materials. Zig-zag can occur when only two layers are present, the layers are thick (~500-l000ìm), and in some cases even when adjacent layers are the same material.
The mechanisms responsible for the zig-zag and scattering instabilities have not yet been conclusively identified. A speculative mechanism is that a normal stress mismatch across the interface of adjacent layers drives the secondary flows. The existence of disturbance wavelengths is assumed and has been used to numerically probe mechanisms of growth and decay [5].
The "wave" instability appears in the extruded sheet as a train of parabolas oriented in the flow direction, each parabola spanning the width of the sheet. A photograph of a sheet sample exhibiting the wave instability is shown in Figures 1 and 2. Like zig-zag and scattering, the wave instability is initiated at an internal interface. However, the mechanism, kinematics, and rheological correlations preceding the onset are poorly understood. Consequently, globally valid protocols for attenuating the wave instability are presently unknown. This then forms the basis for the present work.
Experimental
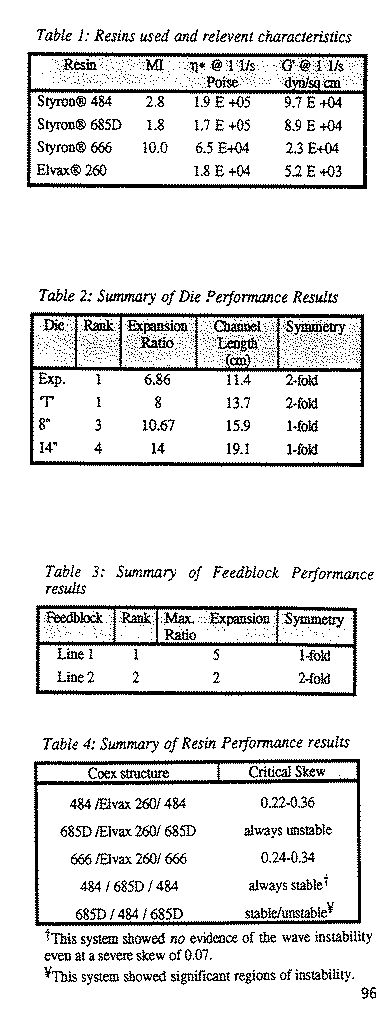
The resins used in this work and relevant characteristics are listed in Table 1. The rheological properties for all the polymeric systems were obtained from oscillatory shear tests conducted on a Rheometrics rheometer (RMS 800).
All the theological data were then shifted using standard techniques (RheCurve software). The viscosities of these materials are depicted in Figure 3 Instability experiments were conducted on two different coextrusion lines. Line 1 was equipped with a 5 layer feedblock. Two 5 cm (2") Killion extruders separately fed the top and bottom layers while two 2.5 cm (1") Killion extruders fed the center and intermediate layers. Line 2 was equipped with a 3 layer feedblock set up for asymmetric structures. The top layer was fed by a 2.5 cm (1") Killion extruder, the middle layer by a 3.2 cm (1.25") TEC extruder and the bottom by a 4.4 cm (1.75") Killion extruder.
Four dies were evaluated: a 20 cm (8") coathanger die (Masterfiex LD-40), a 35 cm (14") coathanger die (Masterfiex RJLD-75), a 30 cm (12") experimental die [6], and a 10cm (4") flow visualization ‘T-slot’ die [7]. Two feedblocks (Line 1 and Line 2) were evaluated as already mentioned. The feedblock study was undertaken to ascertain if upstream effects might be important thus providing an indication of the location of the point of inception of the instability. Feedblock evaluation was conducted by collecting both sheet and logs. Logs are collected by removing the die and taking samples extruded directly from the melt channel.
Each feedblock, die, and material structure was examined at a minimum of two total flow rates. The first flow rate, ~13.6 kg/hr (30 lbs/hr), was chosen to evaluate each system at a constant flow rate. The second flow rate was selected to satisfy the heuristic of a minimum flow rate of 5 lbs/ hr / inch of die width and was, therefore, different for each die.
The performance of a given feedblock, die, or material structure was gauged by the degree of asymmetry attained at a constant total flow rate before the structure exhibited the wave instability. Critical skew was defined as: Skew = thin skin thickness/thick skin thickness. The concept of skew is illustrated in Figure 4. Layer thicknesses were determined by cutting a sample from the sheet along the center line and evaluating the sample by optical microscopy.
A sample was considered unstable if the instability was clearly evident upon visual examination and stable if it was not clearly evident, it should be mentioned that subtle instabilities at an internal interface which appears as waves on the topography are not observable in opaque systems but are in transparent systems.
Results
The results are divided into three sections addressing the topics of die geometry, feedblock, and resin rheology.
A. Die Geometry Study: The die geometry results are shown graphically in Figure 5 and are taken from Line 1. Consider Figure 5 showing the results for the 484/Elvax 260/484 structure. Small values of the critical skew indicate superior performance; that is, greater asymmetry is achievable before the structure exhibits the instability. Skew values smaller than the critical values correspond to unstable sheet. Clearly, the 14" coathanger die exhibits the worst performance always yielding unstable sheet even under nearly symmetric conditions. The 8" coathanger die performs better than the 14" coathanger die and the exponential and T dies exhibit the best performance and are comparable. The error bars on the data points indicate the skew range where the critical skew can be found. The lower limit of the error bars corresponds to a skew value yielding unstable sheet and the higher limit of the error bars corresponds to a skew value yielding stable sheet.
The die performance results are summarized in Table 2. Also shown in the table are the die geometry parameters that follow a trend matching that of the die rank (1 being best and 4 being worst). While many geometric parameters were evaluated, including the contraction ratio, only those shown yielded a consistent trend. The expansion ratio is defined as the ratio of the die width at the exit (lip width) and the channel width at the die manifold entry. The channel length is measured from the feed slot vanes to the die manifold. Each of the dies showed at least one plane of symmetry; the left and right hand sides of the dies are mirror images. Both the T and exponential dies had a second plane of symmetry; the top and bottom halves of the dies are also mirror images. The land of the 8" coathanger die is slightly offset from the centerline and the 14" coathanger die has an offset land and a flow distributor in the die land.
The die geometry results are enlightening. Within the constraints of our experiments, it appears that, the instability is exacerbated by increase in expansion ratio and channel length. It appears that the die geometry can be exploited to attenuate the instability.
There are a few additional points worthy of note. First, the die with the most severe rate of expansion (T die) and the least severe rate of expansion (exponential die) showed the best performance. Manifold spread geometry alone does not appear to be a critical parameter to exploit in order to attenuate the instability as previously thought. Second, the trend between the die rank and the channel length suggest that the instability may indeed be initiated before the die, thus emphasizing the need to study the influence of feed block geometry.
B. Feed Block Study: The feedblock results are shown in Figure 6. Prior studies did not indicate that the feedblock influenced the wave instability; however, these early studies used only opaque resins and did not focus on incipient conditions. Clearly the Line 1 feedblock showed superior performance. While it is inappropriate to draw conclusions regarding the optimal feedblock geometry to prevent the wave instability from only two data points (feedblocks), it is of interest that the feedblock performance results are analogous to the die performance results. These results are summarized in Table 3 where the feedblock performance, expansion ratio, and symmetry trends are tabulated. The feedblock melt channels are equal in length.
Feedblock performance was also examined in the context of the velocity mismatch (ratio of high to low velocity) between adjacent layers. At the condition of incipient stability, the velocity mismatch and skew in the Line 1 feedblock are approximately 6 and 0.3 while the velocity mismatch and skew in the Line 2 feedblock are approximately 10 and 0.5. Since the feedblock with the inferior performance (Line 2) can yield stable sheet at a velocity mismatch greater than can the feedblock with superior performance (Line 1) we conclude that velocity mismatch does not induce the wave instability.
C. Resin Rheology: To facilitate the discussion of the effects of resin rheology, *. and G’ are tabulated for =1s in Table 1. Shown in Table 4 are the resin performance results taken from the T die study on Line 1.
Consider first the Styron/Elvax 260/Styron structures. Styron 484 and Styron 685D have nearly identical dynamic viscosities, yet the performance of these two resins is drastically different. The 484/Elvax 260/484 structure shows a significant region of stability while the 685D/Elvax 260/685D structure is always unstable. A comparison of the 484/Elvax 260/484 and 666fElvax 260/666 structures shows similar performance (to within the resolution of the experiments) even though 666 is ~3 times less viscous than 484. It is apparent from these results that the shear viscosity of the skin is not a defining parameter for the wave instability. These results are not inconsistent with earlier findings where a reduction in the skin viscosity was often found to be beneficial, but not consistently so.
To ascertain if the large disparity in shear viscosity between the skin and core was an exacerbating factor, the 484/685D/484 and 685D/484/685D structures were evaluated. These structures have a shear viscosity ratio of nearly unity. The results are quite surprising; the 484/685D/ 484 structure proved to be stable for all skews tested while the 685D/484/685D structure showed significant regions of instability. No trends are evident between the rheology data in Table 1 and the resin performance data in Table 4.
Since there was obviously a resin effect, it is clear that DMS characterization of the resins was not adequate. Capillary rheometry including the Bagley correction yielded the results shown in Figure 7. A comparison of Figure 7 and Figure 3 shows that the shear viscosity results are consistent and demonstrates that it is not the defining physical property that characterizes resin performance with respect to the wave instability.
The die geometry study and feedblock study both suggest that the extensional (or compressional) rheology of the resins may be important; both die and feedblock performance improved with decreasing expansion ratio. Consequently, Cogswell’s method (8) was used to measure the extensional viscosity of the resins. We do not contend that Cogswell’s method is sufficiently accurate to rely on the extension rate behavior of the extensional viscosity, but it is assumed to yield a valid measure of the magnitude of the extensional viscosity [9]. The results are plotted below in Figure 8.
The significance of the extensional viscosity data is not immediately obvious. However, it can be made clear when the extensional viscosity ratio is evaluated. Table 5 shows two measures of the extensional viscosity ratio, denoted by m, for each of the structures of Table 4. The first ratio is based on the algebraic mean of the extensional viscosity data of each resin, i.e. m = ( Stvron 484)avg/( E1vax 260)avg. This measure was chosen because the extensional viscosity of each of the resins could not be measured at the same extension rate with Cogswell’s method. The second is the ratio of the extensional viscosities at an extension rate as near to 20s’ as was measured. All ratios are reported with the core extensional viscosity in the denominator. The Elvax 260 core structures and the Styron core structures are tabulated separately in order of decreasing performance. Note that either measure of the extensional viscosity ratio yields the same trend.
Consider the data in the context of the Elvax 260 core structures first. Recall from Table 4 that the 484/Elvax 260/ 484 and 666fElvax 260/666 systems exhibited nearly the same performance. Table 5 and Figure 8 show that these resins have extensional viscosity ratios that are nearly the same. The Elvax core structure with the worst performance was the 685D/Elvax 260/685D and it is this system that has the largest extensional viscosity ratio. When the core structure is a Styron material the same trend is observed. These results suggest that when the extensional viscosity of the skin is substantially greater than that of the core, the structure will be susceptible to the wave instability.
Conclusions
The critical skew required to induce the wave instability was found to be feedblock dependent. It was shown that, in some cases, the wave instability can be initiated in the feedblock. Performance was evaluated in the context of feedblock geometry and greater sheet asymmetry was attainable when the feedblock had a small expansion ratio and 2-fold symmetry.
The geometry of the die has been shown to significantly influence whether or not the extruded sheet will exhibit the wave instability. Die expansion ratio, channel length, and symmetry showed a consistent trend with die performance. More severe skews were attainable when the die had a small expansion ratio, a short channel length, and 2-fold symmetry. These results were unaffected by the initiation point of the instability; relative die performance was shown to be independent of the extrusion line and resin structure.
For all cases where data is available it has been shown that structures with a large extensional viscosity ratio or with a large extensional viscosity skin are more susceptible to the wave instability. Two layer structures with large extensional viscosity exhibited the wave instability. Since extensional viscosity is only important in expansion or contraction flows, the feedblock, die and resin results are consistent.
All trademarks used are trademarks of their respective companies. Nothing herein grants or implies any license to practice under patents of The Dow Chemical Company or others.
References
1. W. J. Schrenk and T. Alfrey, "Coextruded Multilayer Polymer Films and Sheet", in Polymer Blends, Vol.2, D. R. Paul and J. R. Newman, editors, Academic Press, 1978.
2. W.J. Schrenk, N.L Bradley, T. Alfrey and H. Maack, Polym. Eng. Sci., 18, 620, (1978).
3. C. D. Han and R. Sherry, Polym. Engr. and Sci., 18, 180 (1978).
4. R. Ramanathan, W.J. Schrenk and I. Whearley, USP 5,269,995 (1993).
5. C. S. Yih, J. Fluid Mech., 27, 337, (1967).
6. R. Shanker, R. Ramanathan, W.J. Schrenk, SPEANTEC preprints, Boston, (1995).
7. R. Ramanathan, S. Jons, D.L. Headley, W.J. Schrenk, SPE ANTEC preprints, San Francisco (1994).
8. F.N. Cogswell, Polym. Engr. Sci., 12, 64 (1972).
9. Laun H.M. and H. Schuch, J. of Rheology, 33 (1), 119, (1989).
 Tables |
Figure 1: Topographical view of "Wave" pattern instability in 3 layer structure
 Figure 1 |
Figure 2: Spatial progression of "wave" pattern instability in 3 layer structure
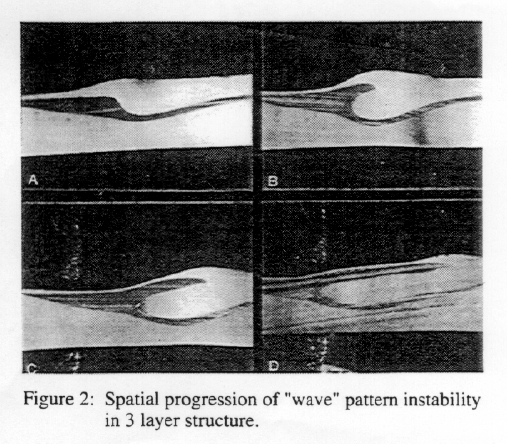 Figure 2 |